- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How should I compare and validate the mean and spread of various distributions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How should I compare and validate the mean and spread of various distributions
Would like to seek some advice here.
I have a baseline/ nominal distribution and I would like to make a comparison among distributions A, B, C & D to see if their mean and spread are equivalent/ comparable to the baseline distribution. What will be the most effective measure that I can use in JMP 13 ?
Thank you,
Ann Ann
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How should I compare and validate the mean and spread of various distributions
Many common hypothesis tests (e.g., t-tests, one-way ANOVA) are parametric tests of a difference in the population mean. The Oneway platform (select Analyze > Fit Y by X) performs both of these tests. You can use a multiple comparison method such as Dunnett's test when you have a control population if you decide that there is a significant difference with the ANOVA.
This platform also provides parametric tests of the spread. Click the red triangle next to Oneway and select Unequal Variance. Unfortunately, there are no multiple comparison methods for the spread.
See Help > Books > Basic Analysis and then the chapter specifically about Oneway platform.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How should I compare and validate the mean and spread of various distributions
There are numerous possibilities for analyzing what you described: 1 to 100 tests with 5 conditions on each test where each result is a "distribution". The appropriate analysis depends upon how the data were collected.
- For example, suppose each test represents a batch, same source material, or same time frame and conditions A, B, C, D and Baseline were run on each. In this case, Test/Batch should be treated as a blocking factor (JMP Oneway with Test as a block) or as a multivariate response model.
- The "distribution" of each test and condition will also modulate which analysis to perform.
My suggestion is to find someone within your organization or university (or near by university) to get some statistical consulting advice.
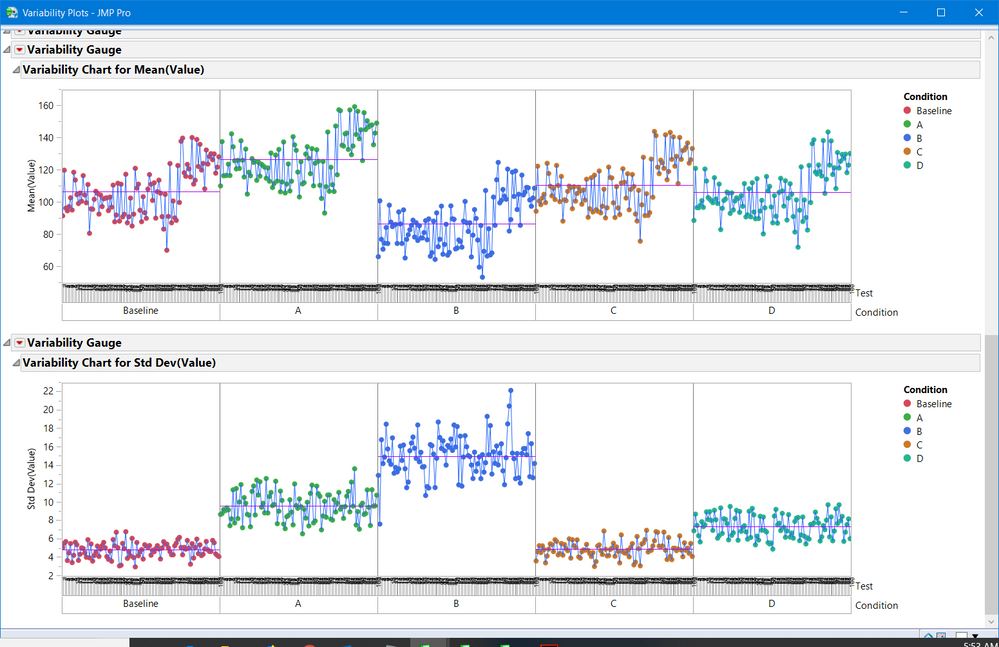
I have no idea how your data were collected so the attached example data table with embedded graphs are meant to show you visual and analytical possibilities using JMP. The JMP table contains simulated data for 100 tests, each run with A, B, C, D and Baseline conditions and the "distribution" is 20 measurements that represent random effects ( versus fixed effects: such as, measurements taken on fixed locations of an object; or taken at a specific sequence of time intervals, such as a drug efficacy test where measurements are collected at 0, 1hr, 5 hrs, etc.). The simulation's test-test variation is large; a shift was added after after run 75 to make the effect even more visible.
The attached table contains 3 embedded scripts:
- Variability Chart of Value - A plot of the raw data grouping by Test, Condition. On the right hand side of the X-Axis click on Test and drag it to Condition.
- Summary Plots - Creates the table Test Summary that computes the "distribution" mean and stdev of each Test/Condition, then plots variability charts comparing "distribution" means and std dev grouping by Test, Condition then Condition, Test; four plots in all( see the two Condition,Test plots below).
- Dunnett Comparison with Test as a Block Factor - This script uses the Test Summary table and a Oneway ANOVA, using Test as a Block. This removes the test-test factor and performs a Oneway comparison of the block differences.
Note I built the simulation so that Baseline and D have the same means (C is not too far off), and Baseline and C have the same std dev.
Please keep in mind, if your experiments were not run like this likely #3 is not the best analyses, however, graphs like #1 and #2 should provide you with some insight to your experimental results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How should I compare and validate the mean and spread of various distributions
Many common hypothesis tests (e.g., t-tests, one-way ANOVA) are parametric tests of a difference in the population mean. The Oneway platform (select Analyze > Fit Y by X) performs both of these tests. You can use a multiple comparison method such as Dunnett's test when you have a control population if you decide that there is a significant difference with the ANOVA.
This platform also provides parametric tests of the spread. Click the red triangle next to Oneway and select Unequal Variance. Unfortunately, there are no multiple comparison methods for the spread.
See Help > Books > Basic Analysis and then the chapter specifically about Oneway platform.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How should I compare and validate the mean and spread of various distributions
I would suggest starting with a more general approach. You should overlay the distributions and compare them visually. Mean and spread are summary measures and they may or may not match the most salient features of the distributions. Depending on what the distributions look like, you may be able to use concepts such as stochastic dominance which compare the shapes of the distributions more generally than just using the first two moments of the distributions. The cumulative distributions are another way to view the comparisons that might yield useful insights.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How should I compare and validate the mean and spread of various distributions
I always start with graphs to ensure it is a fair comparison. To add to @dale_lehman's recommendations, I suggest to plot the data by sequence (time) or other factors that might be salient to these distributions, for example if looking at the price of homes, looking by location or features (# of rooms) etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How should I compare and validate the mean and spread of various distributions
Thank you very much for the suggestions. Appreciate them very much.
Another quick question...
Should I have tests 1 to 100, and every test has distributions A, B, C and D with 1 baseline distribution. What will be a quick indicator or measure that I can use to see if there is a mismatch in the mean performance ? And based on that indicator, follow up actions will be taken to investigate further. For example, if I have 2 distributions per test, I may activate the T test to check on the T ratio and P value. But if I have several distributions per test, what would be a simpler way to do a quick check ? Will Anova F ratio be a good indicator?
Thank you and Happy New Year.
Ann Ann
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How should I compare and validate the mean and spread of various distributions
There are numerous possibilities for analyzing what you described: 1 to 100 tests with 5 conditions on each test where each result is a "distribution". The appropriate analysis depends upon how the data were collected.
- For example, suppose each test represents a batch, same source material, or same time frame and conditions A, B, C, D and Baseline were run on each. In this case, Test/Batch should be treated as a blocking factor (JMP Oneway with Test as a block) or as a multivariate response model.
- The "distribution" of each test and condition will also modulate which analysis to perform.
My suggestion is to find someone within your organization or university (or near by university) to get some statistical consulting advice.
I have no idea how your data were collected so the attached example data table with embedded graphs are meant to show you visual and analytical possibilities using JMP. The JMP table contains simulated data for 100 tests, each run with A, B, C, D and Baseline conditions and the "distribution" is 20 measurements that represent random effects ( versus fixed effects: such as, measurements taken on fixed locations of an object; or taken at a specific sequence of time intervals, such as a drug efficacy test where measurements are collected at 0, 1hr, 5 hrs, etc.). The simulation's test-test variation is large; a shift was added after after run 75 to make the effect even more visible.
The attached table contains 3 embedded scripts:
- Variability Chart of Value - A plot of the raw data grouping by Test, Condition. On the right hand side of the X-Axis click on Test and drag it to Condition.
- Summary Plots - Creates the table Test Summary that computes the "distribution" mean and stdev of each Test/Condition, then plots variability charts comparing "distribution" means and std dev grouping by Test, Condition then Condition, Test; four plots in all( see the two Condition,Test plots below).
- Dunnett Comparison with Test as a Block Factor - This script uses the Test Summary table and a Oneway ANOVA, using Test as a Block. This removes the test-test factor and performs a Oneway comparison of the block differences.
Note I built the simulation so that Baseline and D have the same means (C is not too far off), and Baseline and C have the same std dev.
Please keep in mind, if your experiments were not run like this likely #3 is not the best analyses, however, graphs like #1 and #2 should provide you with some insight to your experimental results.

Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us

