- JMP User Community
- :
- Discussions
- :
- How do I test statistical significance of a time series trend line using JMP GUI
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How do I test statistical significance of a time series trend line using JMP GUI
Hi - I am trying to test whether my time series trend line is statistically significant. I'd also like to test for seasonal trends. I'd like to do this within the JMP GUI.
My data are dissolved "chemical A" vs time sampled, and I have data approximately monthly for 4 years.
Thanks in advance!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I test statistical significance of a time series trend line using JMP GUI
Assuming you're using the Analyze...Specialized Modeling...Time Series platform: while there isn't a way to see if the entire trend line is statistically significant, you can check if the individual parameters are significant in most of the Parameter Estimates tables. In ARIMA models, these estimates can be useful for "sneaking up" on a model for which all the parameters are significant. The Seasonal ARIMA option takes seasonal trends into account.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I test statistical significance of a time series trend line using JMP GUI
My data are nearly, though not exactly, monthly over a 4 year span. I want to evaluate whether 1) the time-series of PFMOAA is trending upward, downward, or not at all; 2) PFMOAA fluctuates seasonally.
When I attempt to use the analyze.....modeling.....time series, JMP says the "data must be sorted by time and be evenly spaced". This seems unrealistic. My data are not collected at perfectly spaced time intervals. How often would this ever be the case. I may not be on the right track here but am attempting to answer the two questions above.
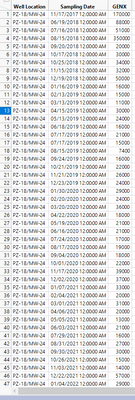
A screen capture of (part of) my data is below.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I test statistical significance of a time series trend line using JMP GUI
Two easy things to do, that may or may not be sufficient for your purposes:
1. If the sampling times only vary by a few days but are roughly monthly, create a month/year variable to use in your time series analysis (this would be evenly spaced).
2. If the precise data/time of the data collection is important, you can try regression (simple or multiple, if you have additional predictors) with the time as one of the factors (entered as a continuous variable) - it's coefficient should reveal something about the time trend. Since it is likely that there may be autocorrelation, you might try transforming the Y variable to first order differencing. That might be a more legitimate model - but I think the time trend will then be picked up in the intercept rather than the time coefficient (that latter would indicate if there is a change in the time trend).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How do I test statistical significance of a time series trend line using JMP GUI
Even time spacing of observations is not at all unusual for many physical, economic, sociologic or demographic situations. Is your null hypothesis that the trend component slope = 0? Vs. and alternative slope does not equal zero? With uneven time spacing just fit an index predictor to the response and test for your hypothesis. You do not specify your alpha level so at some alpha level you will have to reject the null hypothesis.
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us