- Due to inclement weather, JMP support response times may be slower than usual during the week of January 26.
To submit a request for support, please send email to support@jmp.com.
We appreciate your patience at this time. - Register to see how to import and prepare Excel data on Jan. 30 from 2 to 3 p.m. ET.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How can I run the test of homogeneity of variance (Levene's test)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How can I run the test of homogeneity of variance (Levene's test)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How can I run the test of homogeneity of variance (Levene's test)?
It seems that we are getting deeper and deeper into analysis and modeling. That situation is the realm of training, not the realm of on-line discussions.
There are many references that cover residual analysis. This analysis is aimed at verifying the assumptions of the test or model. That verification includes assumptions of homogeneity.
One thing that is commonly done is to plot the residuals as a distribution and versus the predicted response and the predictors. The linear regression assumes that the residuals are normally distributed with constant variance.
I encourage you to continue to submit questions here, but some requests may not be possible to satisfy in this format.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How can I run the test of homogeneity of variance (Levene's test)?
Thank you very much, Mark!
As I understood your advice, in the Fit Model -> Fit Group report, I selected Save Columns -> Residuals. After that I selected Analysis-> Distribution and I chose "Residual column" as Y Column By Timepoint (I have a repeated-measures design), then I plotted the distribution. In this case, I didn't insert the predicted response and the predictors into By.
The second step was analysing the residuals versus the predicted response and the predictors. I selected Analysis -> Fit Y by X, and I chose "Residual column" as Y Column, "the predicted response and the predictors" as X, Factors and By Timepoint.
Am I correct in those procedures? If not, please let me know the step procedures to perform that residual analysis.
Thank you very much for your help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How can I run the test of homogeneity of variance (Levene's test)?
Yes, you have the right idea. In addition to the Distribution analysis, you could use Oneway to look at residuals by time point.
I highly recommend two of our courses:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How can I run the test of homogeneity of variance (Levene's test)?
Hi Mark, thank you for your post.
In the test of homogeneity of variance, I need to get a F-ratio and p-value from Levene's test. Thus, how could I get that information in that procedure you suggested, please?
Don't you think even for approaching I cannot consider that initial option to perform the homogeneity of variance using Oneway ANOVA? I mean JMP performs the outcome considering the timepoints and evaluates the following parameters:
Level | Count | Std Dev | MeanAbsDif to Mean | MeanAbsDif to Median |
T1 | N | SD1 | X1 | Y1 |
T2 | N | SD2 | X2 | Y2 |
T3 | N | SD3 | X3 | Y3 |
where N is the number of participants.
Based on those above parameter, it shows the result from "Levene's test".
Thank you for your attention.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How can I run the test of homogeneity of variance (Levene's test)?
Reinaldo,
When there are complex effects, I typically recommend finding delta, the difference of the measured response minus the mean of fixed effects and time. To visualize these effects, create a column Mean Effect using the formula,
Col Mean( :Y, :Treatment, :Time )
Then create the column delta, Y - Mean effect. Next call up the Variability chart and plot Y, Delta and Mean Effect by Treatment, Time, etc. This provides a visual representation of the variability. Next combine columns representing the effects, call the new column Effects. Now perform a Oneway Analysis of Variance and test for Unequal Variances.
Many significance tests, especially for small sample group sizes or very large group sizes, might not flag or over flag. If there are at least 5 to 10 per group, look at the ratio of the max stdev to the min stdev and if the ratio is more than 3 then it is showing unequal variance with 11-20 if the ratio is more than 2 and no outliers, then varainces are likely unequal.
JMP has a rich repeated measures example data table Cholesterol Stacked.jmp. I modified it per these suggestions and added two scripts prefixed by gzm: gzm - Variability and gzm - Oneway. This study is looking at the effects of two (A and B) cholesterol lowering drugs vs. a control and a placebo. See attached file. Note the Levene's test in the report.
As you might expect those getting an effective treatment will have more variation than those that are not (a person with higher cholesterol to begin with might have bigger drop, and drugs do have the same effect on all).
The cholesterol data is also used for a Manova analysis with tests for unequal covariance (sphericity tests).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How can I run the test of homogeneity of variance (Levene's test)?
Hi @gzmorgan0,
Thank you very much for your help and explanation. Excellent! I am doubt about some steps in your procedure, as follows:
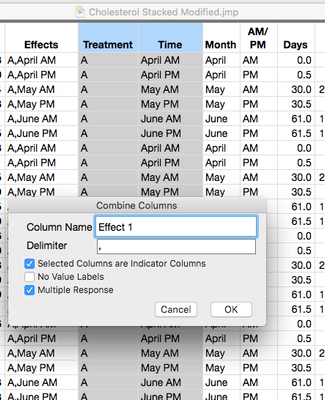
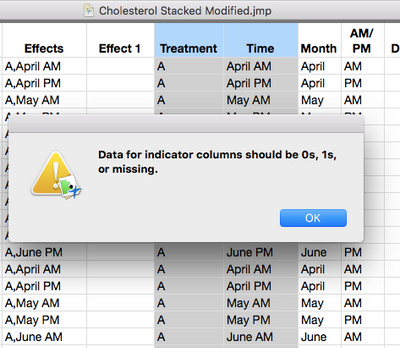
1. For testing how to combine columns, I tried to repeat your step and it didn't work. I followed the steps in the URL: file:///Applications/JMP%2014%20SW.app/Contents/Resources/en.lproj/JMPHelp/index.html#page/jmp%2FUG_EnterEditManageData_46.html, but an error messages was displayed (please, see the screenshots).
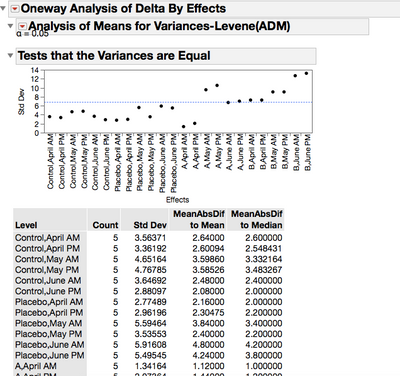
2. Regarding the min stdev and max stdev, do you refer to look at the "Test that the variance is equal" (screenshot)? I mean I need to compare each stdev given in that table to the "blue" stdev and verify if it exceds 3 stdev? By the way, I don't find the exact value of "blue" stdev in the Oneway ANOVA, but only that blue line.
3. As for the attached Fit Model scripts in your JMP file, what exactly should I take information from there?
Thank you very much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How can I run the test of homogeneity of variance (Levene's test)?
To make the combined columns uncheck Indicators and multiple response.
From the attached scripts you should look at the data. From the Cholesterol Stacked data the variance is much larger for May and June for :Treatments levels A and B. Also I look for equal variances for the first time period. For a repeated measures, if one group's variance is much larger (or smaller) than the other groups' variance, this could be an indication of bias in the groups.
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us