- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How PCA on correlations standardizes?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How PCA on correlations standardizes?
I have a confusing issue that I am trying to sort out, but having trouble finding an answer to anywhere. I am using JMP to run PCA on corrections using REML Estimation. I know that doing a PCA on correlations standardizes the data in some way and I am not sure how. Does anyone know how?
I am trying to understand how because I am having trouble interpreting my results without knowing this. Specifically, my component1 variable is essentially an estimate of size of bedforms created by plants, and I am regressing it with another variable that is plant size, factoring in a categorical variable (plant species) and looking at the intercepts and slopes. I already know that one of my 3 plant species has the lowest size values for all the things that are loaded into the component1, yet I am getting more positive values for that plant and more negative values for my two larger plant species. Any thoughts here? The magnitude of the intercepts is right I think, it's just flipped in that the one that should have smaller values is actualyl less negative and then with this issue I am having trouble determining how to interpret any variables regressed against this component 1. I hope that I explained this well enough.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
See Help > Books > Multivariate Methods > Principal Components. The following excerpt explains:
--------------------------------------------------------
The scaling of the loadings and coordinates depends on which matrix you select for extraction of principal components:
-
– For the on Correlations option, the ith column of loadings is the ith eigenvector multiplied by the square root of the ith eigenvalue. The i,jth loading is the correlation between the ith variable and the jth principal component.
-
– For the on Covariances option, the jth entry in the ith column of loadings is the itheigenvector multiplied by the square root of the ith eigenvalue and divided by the standard deviation of the jth variable. The i,jth loading is the correlation between the ithvariable and the jth principal component.
-
– For the on Unscaled option, the jth entry in the ith column of loadings is the itheigenvector multiplied by the square root of the ith eigenvalue and divided by the standard error of the jth variable. The standard error of the jth variable is the jth diagonal entry of the sum of squares and cross products matrix divided by the number of rows (X’X/n).
--------------------------------------------------------
The PCA on correlations centers and scales each variable before extracting the components. Hope that this explanation helps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
Principal components are a new axis system. They are a linear combination of the original variables under several constraints. I think that the answer is that the signs of the components are arbitrary. That is, another linear combination with opposite signs would also meet the same constraints and the component would still be valid.
This is a common question. For example, see another explanation here.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
Hello @Mark_Bailey ,
Thank you for the helpful replies. I think that I am starting to understand, bu I am still very confused. I am mostly confused about the notion that direction (+/-) doesn't matter in the PCA and still not sure how I am getting both positive and negative values for my PCA and this makes it so that I am very confused about interpretation. Attached is a part of the dataset i'm workin on that brought this up. I performed a PCA on NbHt, Vol, and Area and saved the principal components. All 3 PC from that test are saved. I did a seperate PC on plant traits that represents size saved as plant mopho PC1. I then used the fit model platform to perform and ANCOVA with PC1 as my dependent variable, and my independent variables are speces (which are 3 plant species - categorical), plantMorphoPC1, and theur interaction. When I do this, the intercept for specis CK is greater than the other two though the results should be the opposite in that both the other two species should be indicating greater intercepts than CK.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
I am trying to answer your last question but I need to return to your original post for clarification. You said, "Specifically, my component1 variable is essentially an estimate of size of bedforms created by plants, and I am regressing it with another variable that is plant size, factoring in a categorical variable (plant species) and looking at the intercepts and slopes. I already know that one of my 3 plant species has the lowest size values for all the things that are loaded into the component1, yet I am getting more positive values for that plant and more negative values for my two larger plant species." I want to be sure of what you found because you have two steps: PCA and linear regression.
Why did you say, "component1 variable is essentially an estimate of size of bedforms created by plants?" What information were you using to say such a thing? Something from the PCA?
What do you mean by, "I already know that one of my 3 plant species has the lowest size values for all the things that are loaded into the component1?" Are you looking at the loadings? These are correlations between the original variables and the new components. Do you mean magnitude (i.e. absolute value) or signed scale (i.e., -1 is less than +1)?
Can you post the PCA results and the regression results to which you referred?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
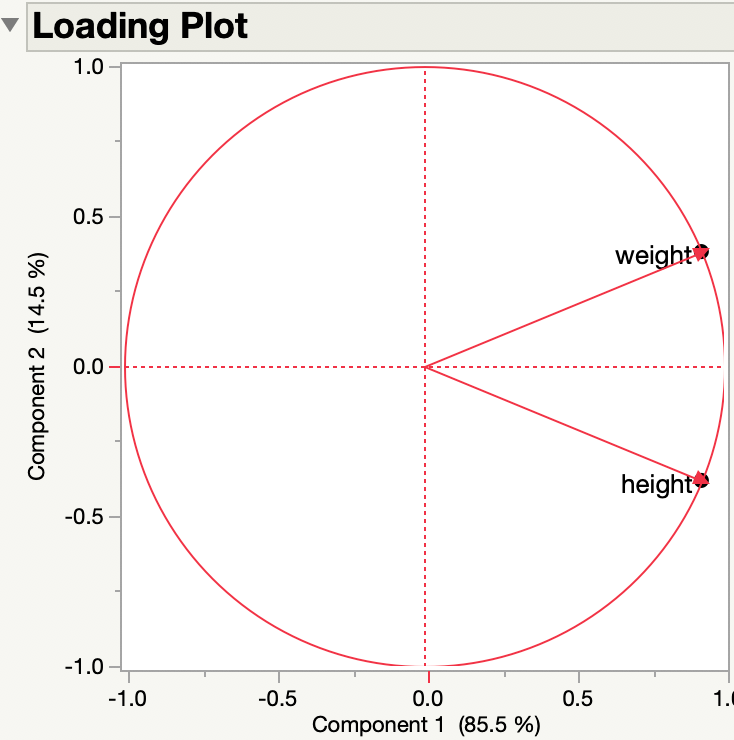
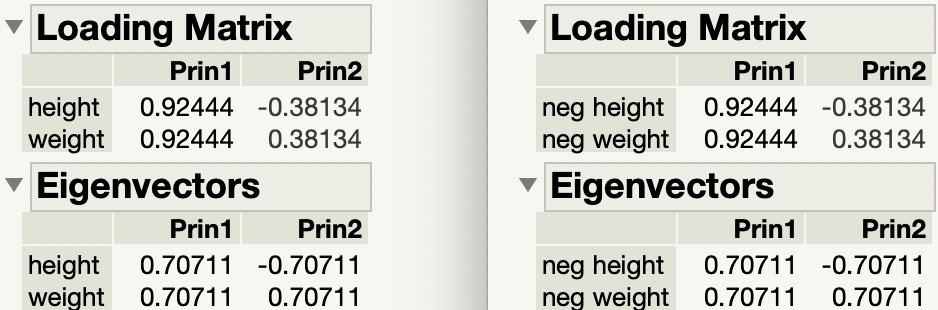
While you consider my request for clarification, here is another illustration of my previous answer. I am using the Big Class data table in the sample data folder. Here are the loadings from the PCA of the two continuous variables, height and weight:
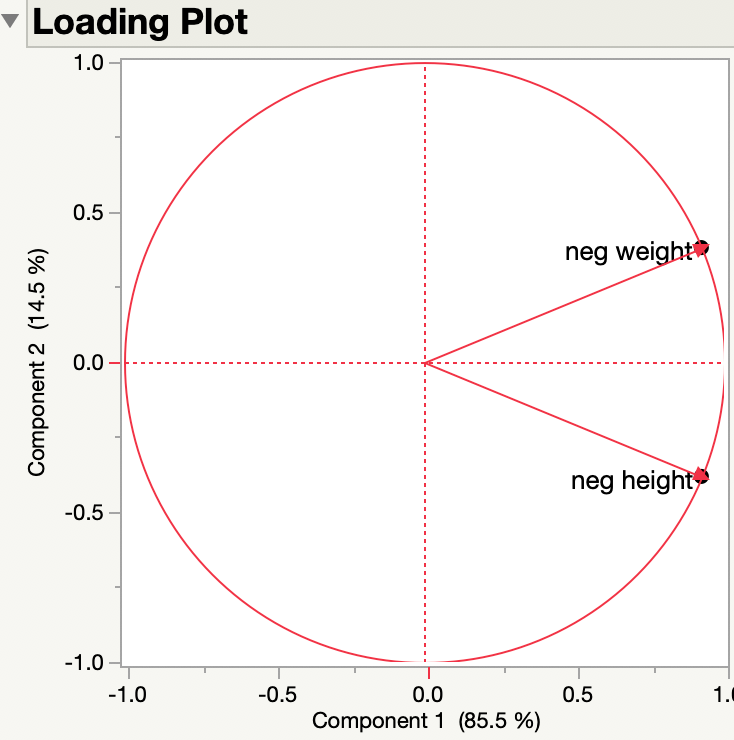
I multiplied both height and weight by -1 and created neg height and neg weight, respectively. Here are the loadings from the PCA of the two continuous variables, neg height and neg weight:
They are the same.
So the sense (negative or positive) of the original variables doesn't matter to the loadings. Here are the side by side results of the original variables and the negated variables:
The principal components represent new dimensions or axes that do not necessarily convey the sign or direction of the original variables.
If you can show your results to which you refer in your previous posts then I think we can address your confusion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
Thank you for posting some of your data, although my request for the results to which you refer earlier would still help.
I assume that the 3 continuous variables were used to create the components. My results are similar but do not agree. Where did the components here come from?
Here is the picture for the 3 continuous variables and the 3 principal components.
So Prin1 is positively correlated with area, vol to Base and NebHt, in decreasing correlation. So the three original variables together capture the size of bedforms?
What is the plant size variable?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
Hi Mark,
Thank you so much for all of your help. By saying that "my component1 variable is essentially an estimate of size of bedforms created by plants" I mean things that descirbe a bedform, ht, area, volume are laoding heavily on it. And by " I already know that one of my 3 plant species has the lowest size values" what i meant is that looking at the variables that load into PC1 for these bedforms just looking at the distribution I know that the means are lower for the one species, but this is the species that I am getting the highest intercept for for PC1. All of the values that go into the PCA are positive and so I am really confused about the positive and negative values that are the PC scores and how you interpret them. Are the scores that are more negative actually more positive in the variables that load on that PCA?
I think that I had saved the wrong PCA values in the intial data set that I posted, but regardless I am confused about the negative PC1 scores and how one actually interprets them.
Best,
Bianca
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
In this dataset, I threw neb Ht, vol, and Area into a PCA and saved the first PC which is PC 1. I have three species. The plant morpho PC is from a PCA analysis of plant metrics the results of which are attached. If you do an ANCOVA you see that the intercept is greatest for CK, but if you look at the distribution of the variables that feed into PC1 then you see it is equal to the others for the most prt, but in an ANCOVA it has a much higher intercept and more positive value and I do not understand why
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How PCA on correlations standardizes?
I calculated the principal components as you described and confirmed you PC 1 so that I am not replying about something different.
I used the linear model PC 1 = intercept + Species + Plant Morpho PC + Species * Plant Morpho PC. Is that what you mean by "if you do an ANCOVA?" I decided that the interaction term is not significant and removed it.
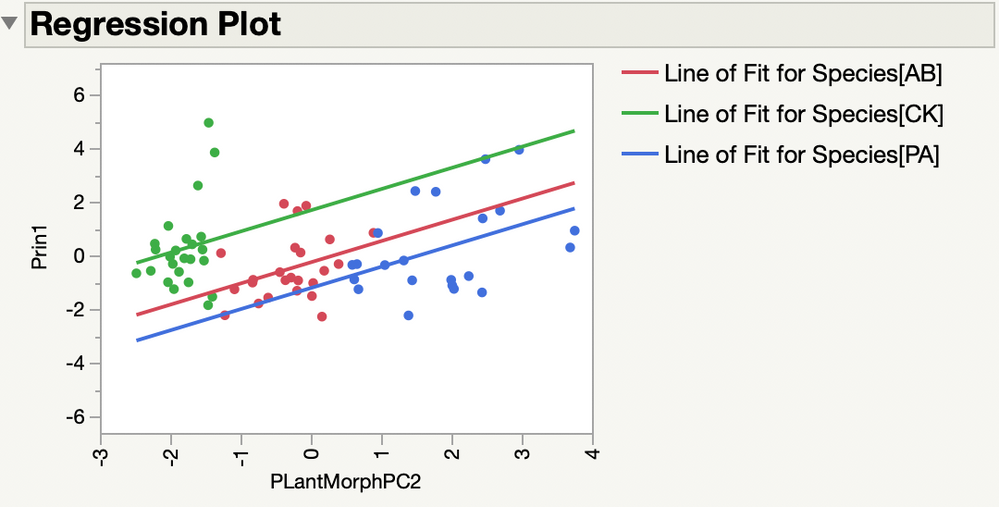
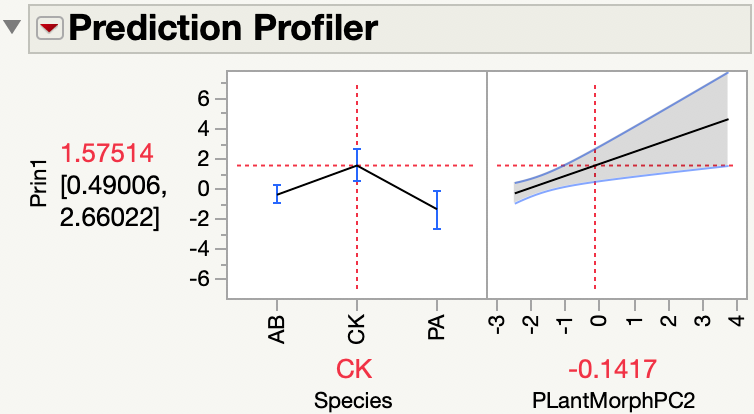
I looked at the regression plot and the prediction profiler to understand the model.
I see that Prin1 is higher for Species=CK as you said. Did you expect no difference between Species?
Principal components find new dimensions that maximize the variation from the original variables (length, area, volume). This new response should make a difference among species easier to detect.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us