- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How JMP calculates confidence interval for a linear fit model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How JMP calculates confidence interval for a linear fit model
For the following set of data,
| X | Y |
| 7.9 | 115 |
| 13 | 154 |
| 10.8 | 156 |
| 11.6 | 182 |
| 10.5 | 124 |
| 11.1 | 157 |
| 8.8 | 129 |
| 11.9 | 181 |
| 11.1 | 164 |
| 9 | 122 |
| 7.4 | 100 |
| 6.9 | 86.2 |
| 9.4 | 118.9 |
| 7.2 | 94.2 |
| 8.8 | 114.3 |
| 7.1 | 104.9 |
| 12.4 | 181.5 |
| 12.1 | 166.1 |
| 15.1 | 166.1 |
| 14.2 | 157.7 |
one can generate a linear fit model as shown below:
Linear Fit
Y = 24.522739 + 11.068566*X
Summary of Fit
RSquare 0.743712
RSquare Adj 0.729474
Root Mean Square Error 16.17783
Mean of Response 138.695
Observations (or Sum Wgts) 20
The question I have is: how should I go about and generate the 99% confidence intervals for the projected Y when X = 11.8 and 12.7? Or even better if you could elaborate the details on how JMP calculates the confidence intervals (such as, 95%, 99%) for a linear fit model.
Many thanks in advance!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Second answer:
- No, it is not more appropriate to use the prediction interval if you are estimating or testing the expected value (or mean) of the response with an interval.
- Yes, it is more appropriate to use the prediction interval if you are estimating a proportion of the population.
They are both correct and both appropriate, depending on what you want to estimate or test. They answer different questions. They are not used for the same purpose. The former is for the statistic and the latter is for the data.
BTW, you can easily visualize either one or both of these intervals when you fit the line in Bivariate. Use same menu under the plot and select Confid Shaded Fit or Confid Shaded Indiv. One is related to the uncertainty in the sample statistic (regression line) and the other is related to the uncertainty of individual observations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Hi!
to get the predicted values and confidence intervals you would do the following:
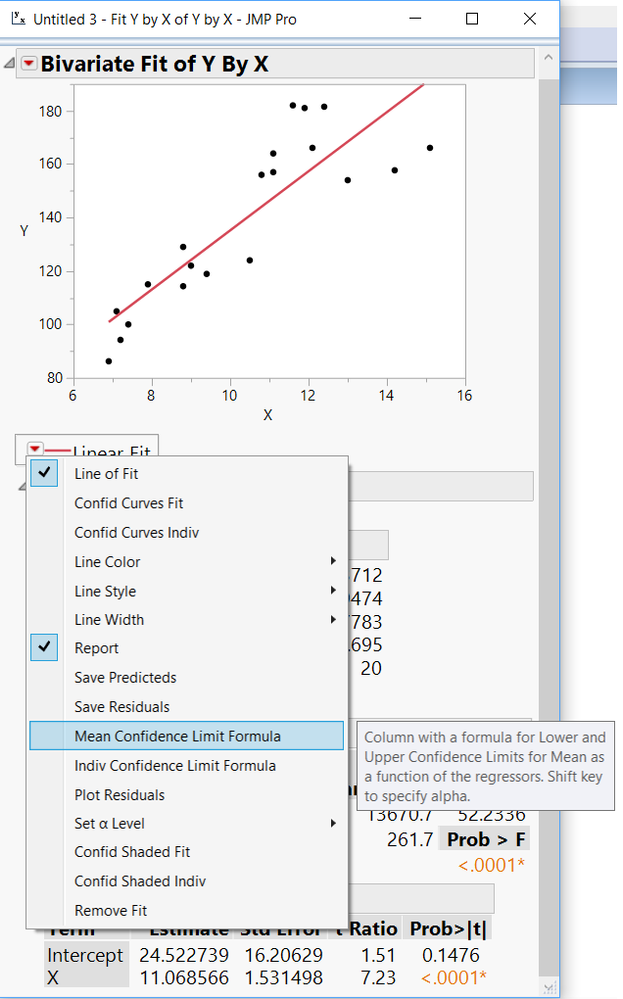
- Use the hotspot (red triangle) next to "Linear Fit".
- You will find a menu entry "Set alpha Level". Set this to 1% if you are interested in 99% confidence.
- Now use the same menu and choose "Save predicteds" and "Mean Confidence Limit formula" (or "Indiv Confidence Limit Formula).
- As a result you will find 3 new columns in the data table.
To see how jmp calculates the prediction/CIs you could just klick on the "+"-symbol on the left hand side (next to the column names).
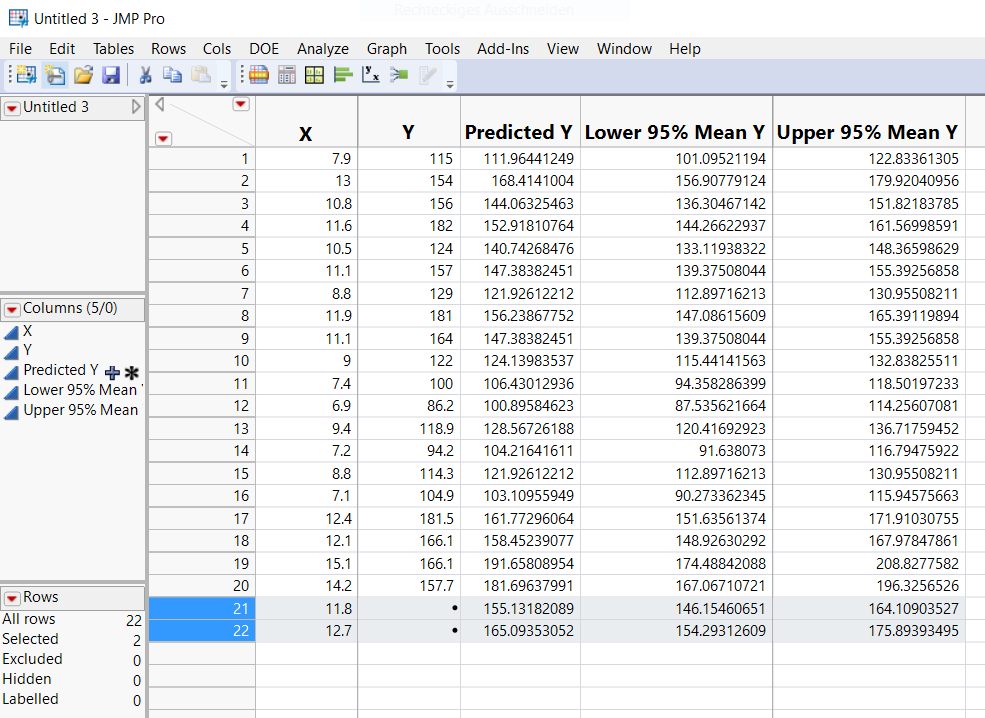
To get the prediction and CI for specific values of X you would just add new rows (like it did in the picture above: Row 21 and 22). JMP will automatically generate the predictions and CI-values for the X-values you enter.
Hope that helps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Thanks for the reply! This was what I did. However, I was puzzled by the Vec Quadratic term in the formula as shown belown and also I was expecting 2.576 multiplying the standard error (for 99% confidence interval calculation instead of 2.878 or 1.96 for 95% confidence interval calculation)
(24.5227390655596 + 11.0685662563684 * :X) - 2.87844047273861 *
Sqrt(
Vec Quadratic(
[1.00352196297906 -0.0924403260280234, -0.0924403260280234
0.00896173786020585],
[1] || :X
) * 261.722077754035
)
2nd quesition: is it more appropriate to use Indiv Confidence Limit Formula than Mean Confidence Limit Formula? If not, why so?
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
The Vec Quadratic() function is an optimized way to perform the matrix computations before applying the scalar multipliers.
You want a two-sided 99% confidence interval, so the probability cutoff on each tail is 0.005%. This calculation with the given 18 degrees of freedom for the error indicates the correct multiplier:
t Quantile( 0.995, 18 ) -> 2.87844047273861
Note that you can select Graph > Profiler and enter all three of the formula columns. You can now change X by dragging or typing over the current value (in red) and entering an exact value. The profilers will give the point estimates, lower and upper bounds.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
I can't answer your second question about which kind of interval is appropriate because you have not stated how you would use or interpret the interval. They are both appropriate but for different questions. It depends on the alternative hypothesis you are trying to test.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Can you show how JMP performs Vec Quadratic calculation? I am looking for a generic equation that JMP uses to calculate prediction interval for OLS. Thanks
Ram
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Help->Scripting Index will tell you that Vec Quadratic(S, X) is a evaluated as Vec Diag(X *S * X`).
Vec Diag(X) returns the diagonal elements of the square matrix as a vector.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Thanks Jeff and Mark for your very quick reply. I got that part. However, in my formula, I have (see attached) 0.395, 0.051, and 0.007 inside first term in Vec Quadratic. I was wondering what these values represent? 0.051 and 0.007 have something to do with the slope, but not very sure. Again, thanks for your assistance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How JMP calculate confidence interval for a linear fit model
Taken directly from the description and explanation I just posted, it is a "symmetric matrix," the "inverse covariance matrix." It refers to the covariance of the parameter estimates, of course.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us