- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How Can I konw if the aliasing exists in the Alias Matrix?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How Can I konw if the aliasing exists in the Alias Matrix?
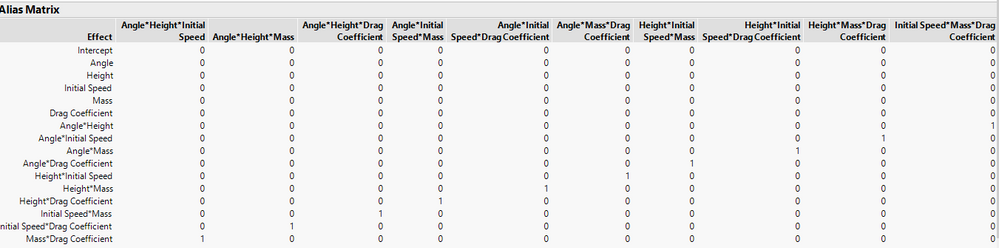
How Can I konw if the aliasing exists in the Alias Matrixthe involving two-way interactions and main effects?
For example, in this Alias Matrix, what does 1 and 0 mean?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How Can I konw if the aliasing exists in the Alias Matrix?
The values in this table are the correlations between the parameter estimates. A 0 means that they are estimated independently. A 1 means that they are confounded. (Each of the parameters is an alias for the same column used to estimate the effect.) A value between 0 and 1 indicates correlation that does not prevent estimation but it will inflate the variance of the estimates, and reduce power.
See Help > Books > Design of Experiments. The information in the Design Evaluation outlines is thoroughly explaned and demonstrated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How Can I konw if the aliasing exists in the Alias Matrix?
From the Screening Design, how do I know if there is aliasing?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How Can I konw if the aliasing exists in the Alias Matrix?
I think you will need to be more specific.
From the menus, are you choosing DOE > Classical > Two Level Screening > Screening Design?
If so, after specifying your factors you are given a choice of choosing a design from a fractional factorial design or to construct a main effects screening design.
If you choose a fractional factorial design, a catalog of designs will appear that provides the resolution. That is usually sufficient, but if not, there is an item in the report window that is labelled Aliasing of Effects. That will show all aliasing up to order 2. If you want higher, click the red triangle at the bottom to choose Show Confounding Pattern to generate to whatever order you wish.
If you choose a main effects screening design, there is an Alias Matrix output in the report which is the correlation matrix that Mark described.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us