- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Hodges-Lehmann Confidence Intervals (1-sided)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Hodges-Lehmann Confidence Intervals (1-sided)
Hi Everyone!
Could someone help me to calculate 1-sided (upper and lower) confidence limits using Hodges-Lehman Confidence Intervals?
I link my post here to another gentlemans' from 2013 since it looks like he didn't get any help in relation to this topic.
https://community.jmp.com/t5/Discussions/JMP-Script-to-do-Hodges-Lehmann/m-p/7208#M7202
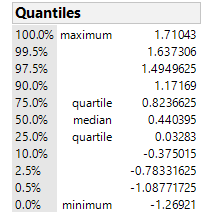
@bwwhite JMP calcualtes a Hodges Lehman piont estimate and upper and lower 2-sided confidence limtis at the confidence level (1-α) of your choosing in the Analyze> Fit Y by X Platform, Under "Nonparametric > Nonparametric Multiple Comparisons > Wilcoxon Each Pair". I include here an example of the output for the particulatar dataset I am looking at:
I asked JMP customer support for their help and they were very kind to offer me some good references which show the mathametics behind the calculation. https://support.sas.com/documentation/cdl/en/statug/63347/HTML/default/viewer.htm#statug_npar1way_a0...
Howevever, In looking at this and workign through it, I'm still beffuddled sadly. :(
The point estimate is just the Median of the the difference column of the Cartesian Join of Data from Column A and Column B, where produced "Cartesian Join" using the Tables > Join function. I was able to prove that this is in fact the right result! It's the first saved data table script in the attached .jmp file.
It's trickier to get the Confidence Limits, Here I have the formula's pretty clear as day, but unfortunately I can't translate them into practical calculation.
Any help would be greatly appreciated!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Hodges-Lehmann Confidence Intervals (1-sided)
Hello Everyone, I wanted to provide some resolution to this thread courtesy of @sseligman at SAS JMP customer support (awesome!), who provided a .jsl script which computes the Hodges-Lehmann Confidence Intervals outside of the Fit Y by X platform.
By simply modifying the alpha level, one can compute the corresponding 1-sided limits vs. JMPs default 2-sided limits. In addition, this script offers the benefit of calculating these non-parametric limits both with and without a so-called "continuity-correction" which JMP employs by default, and SAS does not. This could be particularly useful for you if, for example, you have two groups, Group 1 and Group 2, and you are computing intervals for risk-assessment accross them for the purpose of estimating what change you would need to apply to an existing specification for Group 1 such that it is remains equally conservative for Group 2. Of course this prespupposes that there is a statistically detectable difference in the location difference accross Groups (and that that difference is of practical importance).
For 1-sided intervals in general, replace "α/2" with "α". So, for 1-sided case Confidence = 1 - α. For 2-sided case, Confidence = 1 - (α/2).
Finally, if you wish to change the order of the difference taken (and the subsequent calculations on the location difference including the CIs) you simply need to change "Ascending" to "Descending" in the below portion of the script:
// Pick up distinct values
sortx = Sort Ascending( x );Here is the complete script, and I am also including it as an attachment.
// Main routine
MainNonParMCP=Function({},{default local},
// Column dialog to get data values
alpha=0.10;
{alpha,ng, xdistinct, x, y}=GetDataMatrix(alpha);
/* ---------------------------------------------------*/
/* for each pair */
OB1=NonparMCP(ng, xdistinct, x, y, alpha, method=1);
/* for all pairs (Steel-Dwass) */
OB2=NonparMCP(ng, xdistinct, x, y, alpha, method=2);
/* comparisons with the control */
OB3=NonparMCP(ng, xdistinct, x, y, alpha, method=3);
/* ---------------------------------------------------*/
/* Bonferroni for Joint Ranking */
/* for each pair */
OB4=BonferroniJointRanking(ng, xdistinct, x, y, alpha, method=1);
/* for all pairs */
OB5=BonferroniJointRanking(ng, xdistinct, x, y, alpha, method=2);
/* comparisons with the control */
OB6=BonferroniJointRanking(ng, xdistinct, x, y, alpha, method=3);
New Window("Result",
OutlineBox("Steel and Steel-Dwass",
OB1,OB2, OB3
),
OutlineBox("Bonferroni for Joint Ranking",
OB4,OB5, OB6
)
)
);
//
// Invoke column data dialog box, and
// get data values from a data table.
//
GetDataMatrix = Function(
{alpha},{default local},
dt = Current Data Table();
If( Is Empty( dt ),
dt = Open()
);
If( Is Scriptable( dt )==0,
Dialog( "Please open a data table before running this script" );
Throw();
);
// Column Dialog
dlg = Column Dialog(
"Select X and Y Column",
ycol = ColList( "Y, Continuous", DataType( numeric ), MinCol( 1 ), MaxCol( 1 ) ),
xcol = ColList( "X, Nominal", MinCol( 1 ), MaxCol( 1 ) ),
HList("Alpha : ",alpha =EditNumber(alpha))
);
// If canceled
If( Arg( dlg[N Arg( dlg )] ) != 1,
Dialog( "Canceled" );
Throw();
);
// Make Data
xx = Column( dt, dlg["xcol"] ) << GetAsMatrix;
yy = Column( dt, dlg["ycol"] ) << GetAsMatrix;
x = {};
y = [];
// Exclude missing values or excluded values
For( i = 1, i <= N Row( yy ), i++,
If( Excluded( Row State( i ) ) == 0 & Is Missing( xx[i] ) == 0 & Is Missing( yy[i] ) == 0,
Insert Into( x, xx[i] );
y |/= yy[i];
)
);
// Pick up distinct values
sortx = Sort Descending( x );
/*change "Descending" to "Ascending" in the above line of code to change the order of the groups*/
xdistinct = {};
Insert Into( xdistinct, sortx[1] );
For( i = 2, i <= N Items( sortx ), i++,
If( sortx[i] != sortx[i - 1],
Insert Into( xdistinct, sortx[i] )
)
);
ng = N Items( xdistinct );
If(IsMissing(dlg["alpha"])!=0,
alpha=dlg["alpha"]
);
Eval List( {alpha, ng, xdistinct, x, y} );
);
// Wilcoxon tests and Hodges-Lehman confidence interval for two samples
Wilcoxon_HL=Function({y1,y2,q},{default local},
n1=NRow(y1); /* Sample Size of Group 1 */
n2=NRow(y2); /* Sample Size of Group 2 */
n=n1+n2;
r=RankingTie(y1|/y2);
T1=Sum(r[1::n1]);
T2=n*(n+1)/2-T1;
diff=T2/n2-T1/n1;
stderr=Stddev(r)*Sqrt(1/n1+1/n2);
z=diff/stderr;
If(diff>0,
diffc=max(0,(T2-0.5)/n2-(T1+0.5)/n1),
diffc=min(0,(T2+0.5)/n2-(T1-0.5)/n1)
);
zc=diffc/stderr;
/* Hodges-Lehman: Point estimation and Confidence Interval */
dvec=J(n1*n2,1,.);
k=0;
For(i=1,i<=n1,i++,
For(j=1,j<=n2,j++,
k++;
dvec[k]=y2[j]-y1[i]
)
);
dvec=Sort Ascending(dvec);
/* Point Estimate */
If(Mod(n1*n2,2)==1,
HLEst= dvec[(n1*n2+1)/2] ,
HLEst= (dvec[(n1*n2)/2]+dvec[(n1*n2)/2+1])/2
);
/* Confidence interval without continuity correction */
C = Floor( n1*n2/2 - q*Sqrt(n1*n2*(n1+n2+1)/12));
If(C<1,
L=.;
H=.;
,
L=dvec[C];
H=dvec[n1*n2+1-C]
);
/* Confidence interval without continuity correction */
Cc = Floor( n1*n2/2 -0.5 - q*Sqrt(n1*n2*(n1+n2+1)/12));
If(Cc<1,
Lc=.;
Hc=.;
,
Lc=dvec[Cc];
Hc=dvec[n1*n2+1-Cc]
);
EvalList({diff,stderr,z,zc,HLEst,L,H,Lc,Hc});
);
//Nonparametric comparison
// Method==1 ... For each pair, without continuity correction
// Method==2 ... For all pairs, nonparametric Tukey based on pairwise ranking
// "Steel-Dwass test"
// Mehtod==3 ... Comparison with the control, nonparametric Dunnett based on pairwise ranking
// "Steel test"
NonparMCP=Function({ng, xdistinct, x, y, alpha, method},{default local},
Result=[];
g1Label={};
g2Label={};
n=J(NItems(xdistinct),1,0);
For(i=1,i<=NItems(x),i++,
For(j=1,j<=ng,j++,
If(x[i]==xdistinct[j],
n[j]++;
Break()
);
)
);
/* In order to perform, Steel test (nonparametric Dunnett),
we need to get sample size for each group*/
If(method==3,
ncont=n[1];
nother=Matrix(n[2::NRow(n)]);
rho=(1+ncont:/nother)^(-0.5);
);
/* Calculate Crit. value */
If(
method==1,
q=NormalQuantile(1-alpha/2),
method==2,
q=Tukey HSD Quantile(1-alpha,ng,.),
method==3,
q=DunnettQuantile(1-alpha,Nrow(nother),df=.,rho);
);
/* Loop Start */
For(i=1,i<=ng-1,i++,
If(method==3&i>=2,Break());
For(j=i+1,j<=ng,j++,
gval1=xdistinct[i];
gval2=xdistinct[j];
n1=n[i];
n2=n[j];
y1=[];
y2=[];
For(k=1,k<=NRow(y),k++,
If(
x[k]==gval1, y1|/=y[k],
x[k]==gval2, y2|/=y[k]
)
);
// Caclulate z-value and CI */
{diff,stderr,z,zc,HLEst,L,H,Lc,Hc}=Wilcoxon_HL(y1,y2,q);
// Calculate p-values from z
If(method==1,
p=2*NormalDistribution(-Abs(z));
pc=2*NormalDistribution(-Abs(zc));
,
method==2,
p=Tukey HSD P value(Abs(z),ng,.);
pc=Tukey HSD P Value(Abs(zc),ng,.);
,
method==3,
p=Dunnett P Value(Abs(z),ng-1,.,rho);
pc=Dunnett P Value(Abs(zc),ng-1,.,rho);
);
Insert Into(g1Label,Char(gval1));
Insert Into(g2Label,Char(gval2));
Result|/= (n1||n2||diff||stderr||z||p||zc||pc||HLEst||L||H||Lc||Hc);
)
);
If(
method==1, titleOB="Nonparametric Comparison for Each Pair",
method==2, titleOB="Nonparametric Comparison for All Pairs (Steel-Dwass)",
method==3, titleOB="Nonparametric Comparison for Each Pair (Steel)"
);
OB=OutlineBox(titleOB,
TableBox(
NumberColBox(Char(100*alpha)||"% Critical value",Matrix(q))
),
TableBox(
StringColBox("Group2",g2Label),
StringColBox("v.s. Group1",g1Label),
NumberColBox("n2", Matrix(Result[0,2])),
NumberColBox("n1", Matrix(Result[0,1])),
NumberColBox("Diff in Mean Rank", Matrix(Result[0,3])),
NumberColBox("Std Err", Matrix(Result[0,4])),
NumberColBox("Z", Matrix(Result[0,5])),
NumberColBox("p", Matrix(Result[0,6]),<<Set Format( 7, "PValue" )),
NumberColBox("Z with cc", Matrix(Result[0,7])),
NumberColBox("p with cc", Matrix(Result[0,8]),<<Set Format( 7, "PValue" )),
NumberColBox("Hodges-Lehmann",Matrix(Result[0,9])),
NumberColBox(Char(100*(1-alpha))||"% Lower",Matrix(Result[0,10])),
NumberColBox(Char(100*(1-alpha))||"% Upper",Matrix(Result[0,11])),
NumberColBox(Char(100*(1-alpha))||"% Lower with cc",Matrix(Result[0,12])),
NumberColBox(Char(100*(1-alpha))||"% Upper with cc",Matrix(Result[0,13])),
)
);
OB
);
BonferroniJointRanking=Function({ng, xdistinct, x, y, alpha, method},{default local},
Result=[];
g1Label={};
g2Label={};
ry=Ranking Tie(y);
STotal=Stddev(ry);
n=J(NItems(xdistinct),1,0);
T=J(NItems(xdistinct),1,0);
For(i=1,i<=NItems(x),i++,
For(j=1,j<=ng,j++,
If(x[i]==xdistinct[j],
n[j]++;
T[j]+=ry[i];
Break()
);
)
);
/* Calculate Crit. value */
/* Loop Start */
For(i=1,i<=ng-1,i++,
If(method==3&i>=2,Break());
For(j=i+1,j<=ng,j++,
gval1=xdistinct[i];
gval2=xdistinct[j];
n1=n[i];
n2=n[j];
stderr=STotal*Sqrt(1/n1+1/n2);
diff=T[j]/n2-T[i]/n1;
z=diff/stderr;
If(diff>0,
diffc=Max(0,(T[j]-0.5)/n2-(T[i]+0.5)/n1),
diffc=Min(0,(T[j]+0.5)/n2-(T[i]-0.5)/n1)
);
zc=diffc/stderr;
If(method==1,
p=2*NormalDistribution(-Abs(z));
pc=2*NormalDistribution(-Abs(zc));
,
method==2,
p=Min(1,2*ng*(ng-1)/2*NormalDistribution(-Abs(z)));
pc=Min(1,2*ng*(ng-1)/2*NormalDistribution(-Abs(zc)));
,
method==3,
p=Min(1,2*(ng-1)*NormalDistribution(-Abs(z)));
pc=Min(1,2*(ng-1)*NormalDistribution(-Abs(zc)));
);
Insert Into(g1Label,Char(gval1));
Insert Into(g2Label,Char(gval2));
Result|/= (n1||n2||diff||stderr||z||p||zc||pc);
)
);
If(
method==1, titleOB="Nonparametric Comparison for Each Pair (without adjustment for Joint Ranking)",
method==2, titleOB="Nonparametric Comparison for All Pairs (Bonferonni for Joint Ranking)",
method==3, titleOB="Nonparametric Comparison for Each Pair (Bonferonni for Joint Ranking)"
);
OB=OutlineBox(titleOB,
TableBox(
StringColBox("Group2",g2Label),
StringColBox("v.s. Group1",g1Label),
NumberColBox("n2", Matrix(Result[0,2])),
NumberColBox("n1", Matrix(Result[0,1])),
NumberColBox("Diff in Mean Rank", Matrix(Result[0,3])),
NumberColBox("Std Err", Matrix(Result[0,4])),
NumberColBox("Z", Matrix(Result[0,5])),
NumberColBox("p", Matrix(Result[0,6]),<<Set Format( 7, "PValue" )),
NumberColBox("Z with cc", Matrix(Result[0,7])),
NumberColBox("p with cc", Matrix(Result[0,8]),<<Set Format( 7, "PValue" )),
)
);
OB
);
// Invoke Main Function
MainNonParMCP();
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Hodges-Lehmann Confidence Intervals (1-sided)
Hello Everyone, I wanted to provide some resolution to this thread courtesy of @sseligman at SAS JMP customer support (awesome!), who provided a .jsl script which computes the Hodges-Lehmann Confidence Intervals outside of the Fit Y by X platform.
By simply modifying the alpha level, one can compute the corresponding 1-sided limits vs. JMPs default 2-sided limits. In addition, this script offers the benefit of calculating these non-parametric limits both with and without a so-called "continuity-correction" which JMP employs by default, and SAS does not. This could be particularly useful for you if, for example, you have two groups, Group 1 and Group 2, and you are computing intervals for risk-assessment accross them for the purpose of estimating what change you would need to apply to an existing specification for Group 1 such that it is remains equally conservative for Group 2. Of course this prespupposes that there is a statistically detectable difference in the location difference accross Groups (and that that difference is of practical importance).
For 1-sided intervals in general, replace "α/2" with "α". So, for 1-sided case Confidence = 1 - α. For 2-sided case, Confidence = 1 - (α/2).
Finally, if you wish to change the order of the difference taken (and the subsequent calculations on the location difference including the CIs) you simply need to change "Ascending" to "Descending" in the below portion of the script:
// Pick up distinct values
sortx = Sort Ascending( x );Here is the complete script, and I am also including it as an attachment.
// Main routine
MainNonParMCP=Function({},{default local},
// Column dialog to get data values
alpha=0.10;
{alpha,ng, xdistinct, x, y}=GetDataMatrix(alpha);
/* ---------------------------------------------------*/
/* for each pair */
OB1=NonparMCP(ng, xdistinct, x, y, alpha, method=1);
/* for all pairs (Steel-Dwass) */
OB2=NonparMCP(ng, xdistinct, x, y, alpha, method=2);
/* comparisons with the control */
OB3=NonparMCP(ng, xdistinct, x, y, alpha, method=3);
/* ---------------------------------------------------*/
/* Bonferroni for Joint Ranking */
/* for each pair */
OB4=BonferroniJointRanking(ng, xdistinct, x, y, alpha, method=1);
/* for all pairs */
OB5=BonferroniJointRanking(ng, xdistinct, x, y, alpha, method=2);
/* comparisons with the control */
OB6=BonferroniJointRanking(ng, xdistinct, x, y, alpha, method=3);
New Window("Result",
OutlineBox("Steel and Steel-Dwass",
OB1,OB2, OB3
),
OutlineBox("Bonferroni for Joint Ranking",
OB4,OB5, OB6
)
)
);
//
// Invoke column data dialog box, and
// get data values from a data table.
//
GetDataMatrix = Function(
{alpha},{default local},
dt = Current Data Table();
If( Is Empty( dt ),
dt = Open()
);
If( Is Scriptable( dt )==0,
Dialog( "Please open a data table before running this script" );
Throw();
);
// Column Dialog
dlg = Column Dialog(
"Select X and Y Column",
ycol = ColList( "Y, Continuous", DataType( numeric ), MinCol( 1 ), MaxCol( 1 ) ),
xcol = ColList( "X, Nominal", MinCol( 1 ), MaxCol( 1 ) ),
HList("Alpha : ",alpha =EditNumber(alpha))
);
// If canceled
If( Arg( dlg[N Arg( dlg )] ) != 1,
Dialog( "Canceled" );
Throw();
);
// Make Data
xx = Column( dt, dlg["xcol"] ) << GetAsMatrix;
yy = Column( dt, dlg["ycol"] ) << GetAsMatrix;
x = {};
y = [];
// Exclude missing values or excluded values
For( i = 1, i <= N Row( yy ), i++,
If( Excluded( Row State( i ) ) == 0 & Is Missing( xx[i] ) == 0 & Is Missing( yy[i] ) == 0,
Insert Into( x, xx[i] );
y |/= yy[i];
)
);
// Pick up distinct values
sortx = Sort Descending( x );
/*change "Descending" to "Ascending" in the above line of code to change the order of the groups*/
xdistinct = {};
Insert Into( xdistinct, sortx[1] );
For( i = 2, i <= N Items( sortx ), i++,
If( sortx[i] != sortx[i - 1],
Insert Into( xdistinct, sortx[i] )
)
);
ng = N Items( xdistinct );
If(IsMissing(dlg["alpha"])!=0,
alpha=dlg["alpha"]
);
Eval List( {alpha, ng, xdistinct, x, y} );
);
// Wilcoxon tests and Hodges-Lehman confidence interval for two samples
Wilcoxon_HL=Function({y1,y2,q},{default local},
n1=NRow(y1); /* Sample Size of Group 1 */
n2=NRow(y2); /* Sample Size of Group 2 */
n=n1+n2;
r=RankingTie(y1|/y2);
T1=Sum(r[1::n1]);
T2=n*(n+1)/2-T1;
diff=T2/n2-T1/n1;
stderr=Stddev(r)*Sqrt(1/n1+1/n2);
z=diff/stderr;
If(diff>0,
diffc=max(0,(T2-0.5)/n2-(T1+0.5)/n1),
diffc=min(0,(T2+0.5)/n2-(T1-0.5)/n1)
);
zc=diffc/stderr;
/* Hodges-Lehman: Point estimation and Confidence Interval */
dvec=J(n1*n2,1,.);
k=0;
For(i=1,i<=n1,i++,
For(j=1,j<=n2,j++,
k++;
dvec[k]=y2[j]-y1[i]
)
);
dvec=Sort Ascending(dvec);
/* Point Estimate */
If(Mod(n1*n2,2)==1,
HLEst= dvec[(n1*n2+1)/2] ,
HLEst= (dvec[(n1*n2)/2]+dvec[(n1*n2)/2+1])/2
);
/* Confidence interval without continuity correction */
C = Floor( n1*n2/2 - q*Sqrt(n1*n2*(n1+n2+1)/12));
If(C<1,
L=.;
H=.;
,
L=dvec[C];
H=dvec[n1*n2+1-C]
);
/* Confidence interval without continuity correction */
Cc = Floor( n1*n2/2 -0.5 - q*Sqrt(n1*n2*(n1+n2+1)/12));
If(Cc<1,
Lc=.;
Hc=.;
,
Lc=dvec[Cc];
Hc=dvec[n1*n2+1-Cc]
);
EvalList({diff,stderr,z,zc,HLEst,L,H,Lc,Hc});
);
//Nonparametric comparison
// Method==1 ... For each pair, without continuity correction
// Method==2 ... For all pairs, nonparametric Tukey based on pairwise ranking
// "Steel-Dwass test"
// Mehtod==3 ... Comparison with the control, nonparametric Dunnett based on pairwise ranking
// "Steel test"
NonparMCP=Function({ng, xdistinct, x, y, alpha, method},{default local},
Result=[];
g1Label={};
g2Label={};
n=J(NItems(xdistinct),1,0);
For(i=1,i<=NItems(x),i++,
For(j=1,j<=ng,j++,
If(x[i]==xdistinct[j],
n[j]++;
Break()
);
)
);
/* In order to perform, Steel test (nonparametric Dunnett),
we need to get sample size for each group*/
If(method==3,
ncont=n[1];
nother=Matrix(n[2::NRow(n)]);
rho=(1+ncont:/nother)^(-0.5);
);
/* Calculate Crit. value */
If(
method==1,
q=NormalQuantile(1-alpha/2),
method==2,
q=Tukey HSD Quantile(1-alpha,ng,.),
method==3,
q=DunnettQuantile(1-alpha,Nrow(nother),df=.,rho);
);
/* Loop Start */
For(i=1,i<=ng-1,i++,
If(method==3&i>=2,Break());
For(j=i+1,j<=ng,j++,
gval1=xdistinct[i];
gval2=xdistinct[j];
n1=n[i];
n2=n[j];
y1=[];
y2=[];
For(k=1,k<=NRow(y),k++,
If(
x[k]==gval1, y1|/=y[k],
x[k]==gval2, y2|/=y[k]
)
);
// Caclulate z-value and CI */
{diff,stderr,z,zc,HLEst,L,H,Lc,Hc}=Wilcoxon_HL(y1,y2,q);
// Calculate p-values from z
If(method==1,
p=2*NormalDistribution(-Abs(z));
pc=2*NormalDistribution(-Abs(zc));
,
method==2,
p=Tukey HSD P value(Abs(z),ng,.);
pc=Tukey HSD P Value(Abs(zc),ng,.);
,
method==3,
p=Dunnett P Value(Abs(z),ng-1,.,rho);
pc=Dunnett P Value(Abs(zc),ng-1,.,rho);
);
Insert Into(g1Label,Char(gval1));
Insert Into(g2Label,Char(gval2));
Result|/= (n1||n2||diff||stderr||z||p||zc||pc||HLEst||L||H||Lc||Hc);
)
);
If(
method==1, titleOB="Nonparametric Comparison for Each Pair",
method==2, titleOB="Nonparametric Comparison for All Pairs (Steel-Dwass)",
method==3, titleOB="Nonparametric Comparison for Each Pair (Steel)"
);
OB=OutlineBox(titleOB,
TableBox(
NumberColBox(Char(100*alpha)||"% Critical value",Matrix(q))
),
TableBox(
StringColBox("Group2",g2Label),
StringColBox("v.s. Group1",g1Label),
NumberColBox("n2", Matrix(Result[0,2])),
NumberColBox("n1", Matrix(Result[0,1])),
NumberColBox("Diff in Mean Rank", Matrix(Result[0,3])),
NumberColBox("Std Err", Matrix(Result[0,4])),
NumberColBox("Z", Matrix(Result[0,5])),
NumberColBox("p", Matrix(Result[0,6]),<<Set Format( 7, "PValue" )),
NumberColBox("Z with cc", Matrix(Result[0,7])),
NumberColBox("p with cc", Matrix(Result[0,8]),<<Set Format( 7, "PValue" )),
NumberColBox("Hodges-Lehmann",Matrix(Result[0,9])),
NumberColBox(Char(100*(1-alpha))||"% Lower",Matrix(Result[0,10])),
NumberColBox(Char(100*(1-alpha))||"% Upper",Matrix(Result[0,11])),
NumberColBox(Char(100*(1-alpha))||"% Lower with cc",Matrix(Result[0,12])),
NumberColBox(Char(100*(1-alpha))||"% Upper with cc",Matrix(Result[0,13])),
)
);
OB
);
BonferroniJointRanking=Function({ng, xdistinct, x, y, alpha, method},{default local},
Result=[];
g1Label={};
g2Label={};
ry=Ranking Tie(y);
STotal=Stddev(ry);
n=J(NItems(xdistinct),1,0);
T=J(NItems(xdistinct),1,0);
For(i=1,i<=NItems(x),i++,
For(j=1,j<=ng,j++,
If(x[i]==xdistinct[j],
n[j]++;
T[j]+=ry[i];
Break()
);
)
);
/* Calculate Crit. value */
/* Loop Start */
For(i=1,i<=ng-1,i++,
If(method==3&i>=2,Break());
For(j=i+1,j<=ng,j++,
gval1=xdistinct[i];
gval2=xdistinct[j];
n1=n[i];
n2=n[j];
stderr=STotal*Sqrt(1/n1+1/n2);
diff=T[j]/n2-T[i]/n1;
z=diff/stderr;
If(diff>0,
diffc=Max(0,(T[j]-0.5)/n2-(T[i]+0.5)/n1),
diffc=Min(0,(T[j]+0.5)/n2-(T[i]-0.5)/n1)
);
zc=diffc/stderr;
If(method==1,
p=2*NormalDistribution(-Abs(z));
pc=2*NormalDistribution(-Abs(zc));
,
method==2,
p=Min(1,2*ng*(ng-1)/2*NormalDistribution(-Abs(z)));
pc=Min(1,2*ng*(ng-1)/2*NormalDistribution(-Abs(zc)));
,
method==3,
p=Min(1,2*(ng-1)*NormalDistribution(-Abs(z)));
pc=Min(1,2*(ng-1)*NormalDistribution(-Abs(zc)));
);
Insert Into(g1Label,Char(gval1));
Insert Into(g2Label,Char(gval2));
Result|/= (n1||n2||diff||stderr||z||p||zc||pc);
)
);
If(
method==1, titleOB="Nonparametric Comparison for Each Pair (without adjustment for Joint Ranking)",
method==2, titleOB="Nonparametric Comparison for All Pairs (Bonferonni for Joint Ranking)",
method==3, titleOB="Nonparametric Comparison for Each Pair (Bonferonni for Joint Ranking)"
);
OB=OutlineBox(titleOB,
TableBox(
StringColBox("Group2",g2Label),
StringColBox("v.s. Group1",g1Label),
NumberColBox("n2", Matrix(Result[0,2])),
NumberColBox("n1", Matrix(Result[0,1])),
NumberColBox("Diff in Mean Rank", Matrix(Result[0,3])),
NumberColBox("Std Err", Matrix(Result[0,4])),
NumberColBox("Z", Matrix(Result[0,5])),
NumberColBox("p", Matrix(Result[0,6]),<<Set Format( 7, "PValue" )),
NumberColBox("Z with cc", Matrix(Result[0,7])),
NumberColBox("p with cc", Matrix(Result[0,8]),<<Set Format( 7, "PValue" )),
)
);
OB
);
// Invoke Main Function
MainNonParMCP();
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Hodges-Lehmann Confidence Intervals (1-sided)
I wanted to add one important point of clarification to this post, which is that the Hodges-Lehmann Estimation of Location Shift is decidedly NOT a mean, and therefore the confidence limits estimated on the observed location shift are NOT confidence limits on the mean.
I happened upon this confounding of the mean with the location shift because the typical JMP output lists both the Score Mean Difference and the Hodges-Lehmann Location shift with CIs on the same line (as you can see in my previous posts). The Hodges-Lehmann estimate is strictly:
" Hodges-Lehmann estimate 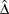 as the median of all paired differences between observations in the two samples, which can be written as
as the median of all paired differences between observations in the two samples, which can be written as
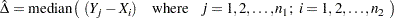 |
as calculated by PROC NPAR1WAY in SAS (see help documentation). Another way of calculating the point estimate is to take the Cartesian Join of Sample 1 and Sample 2 (as separate columns), and then calculate the median of all pairwise diferrerences between Sample 1 and Sample 2. You can prove this to yourself in JMP by creating two columns of data (Sample 1 and Sample 2, respectively; then joining them with Cartesian Join using Tables Join. Calculate the median on Sample 2 - Sample 1 of the cartesian joined table, using the distribution platform and you will get the corresponding Hodges-Lehmann estimate in the Fit Y by X Platform for Sample 1 vs Sample 2.
So then, the CIs are not associated with the mean either. They are associated with some measure of the median, per the formulas given by SAS:
Following Hollander and Wolfe (1999), the asymptotic lower and upper confidence limits for the location shift are
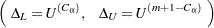 |
where 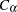 is the largest integer less than or equal to
is the largest integer less than or equal to 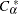 , which is computed as
, which is computed as
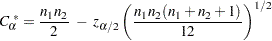 |
where 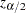 is the
is the 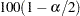 th percentile of the standard normal distribution.
th percentile of the standard normal distribution.
Finally, I think it's important to point out that: Because this is a discrete problem, the confidence coefficient for these exact confidence limits is not exactly 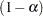 but is at least
but is at least 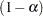 . Thus, these confidence limits are conservative.
. Thus, these confidence limits are conservative.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us