- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Help on a continuous factor values/range for a DOE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Help on a continuous factor values/range for a DOE
Hi, I'm trying to design a DOE for experimenters at my work and I was asked if I can get JMP to include more runs in a specific range of a continuos factor. This factor's values range from 0 to 500 and they think that the range 10 to 100 is most interesting and would like JMP to add more runs within that range than outside it. Is there a way to do this? Any suggestions would help. Thank you.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
I have strong opinions about this issue. I want your experiment to succeed.
The continuous factor range should always be set as wide as possible. Such a design will provide the best estimates for the effects of the factor as well as the highest power for hypothesis tests about these effects for a given number of runs. Limiting the factor range to 10-100 or including these levels within the range of 0-500 will compromise both the estimation and the power. You can see this loss for yourself using the information provided in the Design Evaluation outline after you make the design. You could also use the Compare Design platform to see the difference between the two design options.
(By the way, I do not recommend using a factor range with a lower bound of zero. This practice turns the continuous factor into essentially a categorical factor: absent or present. It is better to use a non-zero value for the lower bound so that the factor is always present, but to varying degrees. That consideration is science and engineering, not statistics.)
If your colleagues insist on including these additional levels then another way, in addition to Ian's answer, is to define this factor with the Discrete Numeric choice. This approach will use a principled design algorithm instead of an ad hoc process of manually adding runs. This way will maximize the information available from your design.
You are designing an experiment, not a test. Use the model, not the design, to find the "most interesting" features or levels. The purpose of an experiment is to provide the best data to fit a given model. The purpose of a test is to observe the response at a particular factor level. They are not the same thing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
This study is a DOE.
The range 10-100 is included in the range of 0-500. So the model will be able to interpolate in the 'sweet spot' range even if the design does not include those particular levels.
I think it comes down to your beliefs about the restricted range of X1: 10-100. If you believe that
- the effect size is large relative to the the standard deviation of the response, say three times larger
- the minimum response occurs within this range
- the expected model is an adequate description over this range
If you believe all these claims are true, then use this range X1: 10-100 instead of X1: 0-500. Why complicate the study?
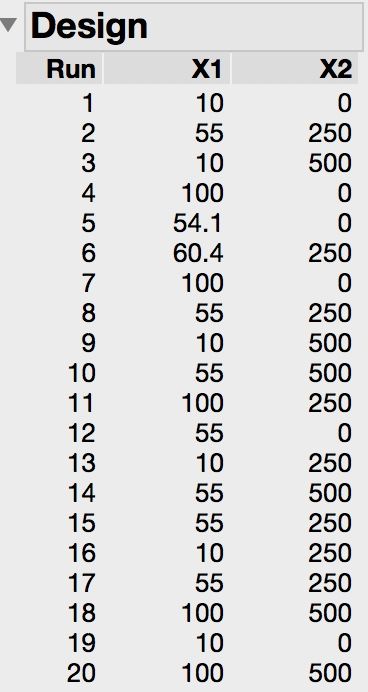
You are able to run a relatively large number of runs to study just two factors. (What about all of the other factors of this response? Keeping them constant? No chance of an interaction effect with them and X1 or X2?) So make a custom I-optimal design for a second order model with X1 and X2 with something like 20 runs. It will out perform the Box-Wilson design (central composite design) and the Box-Behnken design with regard to the data modeling. Here is a design candidate:
Notice that
- replication is a natural result of the larger number of runs
- there are generally three levels for each factor to support the second order model
- a couple of runs set X1 near but off center
- these odd runs increase the optimality
- these odd runs complicate the design (when you run it)
- feel free to change them to the center level with a very small loss in optimality
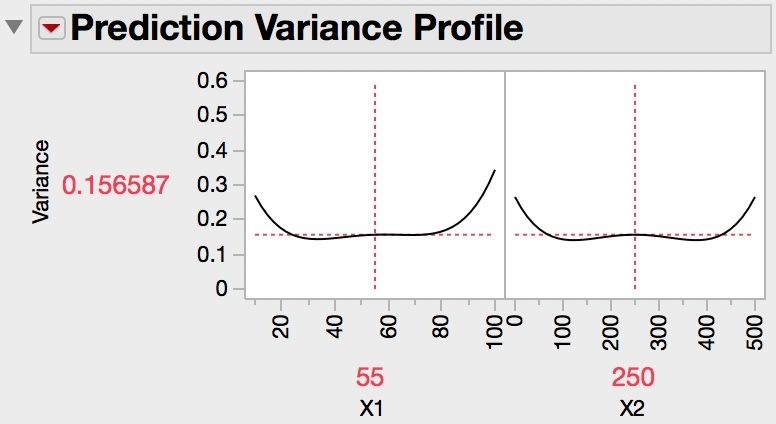
How well does this design perform?
The power is reasonably high if the effect size is at least twice as large as the response standard deviation. This result is a benefit of including 14 runs above the minimum number of runs. You want to use this model to determine the optimum factor settings that will minimize the response.
The variance of your model predictions will be quite low over a large interval of factor levels that is centered in the design space.
So I would drop the distinction about different levels for X1. That distinction comes from a design-centric or testing mindset. A study should come from a model-centric or experimenting mindset.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
In terms of the mechanics, once you have been through the design process with JMP and made a table, you are at liberty to add 'extra' rows to this table by hand with values as you see fit. But whether this is advisable, and if it is, what is the best way to do it, is open to discussion (being determined by what you are prepared to say you know already, and what you are trying to find out).
So, without giving away trade secrets, can you say more about your experimental objectives, and the resources you have available?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
I have strong opinions about this issue. I want your experiment to succeed.
The continuous factor range should always be set as wide as possible. Such a design will provide the best estimates for the effects of the factor as well as the highest power for hypothesis tests about these effects for a given number of runs. Limiting the factor range to 10-100 or including these levels within the range of 0-500 will compromise both the estimation and the power. You can see this loss for yourself using the information provided in the Design Evaluation outline after you make the design. You could also use the Compare Design platform to see the difference between the two design options.
(By the way, I do not recommend using a factor range with a lower bound of zero. This practice turns the continuous factor into essentially a categorical factor: absent or present. It is better to use a non-zero value for the lower bound so that the factor is always present, but to varying degrees. That consideration is science and engineering, not statistics.)
If your colleagues insist on including these additional levels then another way, in addition to Ian's answer, is to define this factor with the Discrete Numeric choice. This approach will use a principled design algorithm instead of an ad hoc process of manually adding runs. This way will maximize the information available from your design.
You are designing an experiment, not a test. Use the model, not the design, to find the "most interesting" features or levels. The purpose of an experiment is to provide the best data to fit a given model. The purpose of a test is to observe the response at a particular factor level. They are not the same thing.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
Maybe to add to (summarize?) what my colleagues have stated, below is the text from a slide I use when explaining DOE to those not familiar with the process.
- Designed Experiments are a systematically generated series of experiments chosen with the goal of being able to understand the relationships and interactions of factors that are thought to impact an observed response.
- What does this mean?
- DOE’s look for what happens to a response when each factor is changed by itself.
- DOE’s also look for what happens when factors are changed together.
- Each experiment in a DOE is calculated to provide the maximum informative value.
- DOE’s are designed to test the widest possible range of settings in the factors.
- DOE’s are more efficient and more powerful than experiments conducted using monothetic analysis.
- The output of a DOE is a mathematical model that can be used to describe the important behaviors of the factors and responses.
- What can you expect from a Designed Experiment?
- Some of the experiments will produce undesirable results (see 2, 4, and 6 above).
- The ”solution” to a particular problem will probably not appear in the experiments (see 6 above).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
Thank you for your help and suggestions. I'll provide you with some extra information on the factors:
continuous X1 (0-500)
continuous X2 (0-5000)
The number of runs we can do are 25 to 50.
The goal is to find the best factor settings/regions to minimize a response Y. We also would like some replicates to asses variability better.
The reason 10 to 100 is important for X1 is because of historical data showing that this range affects the response the most. A custom design in JMP for an RSM model will not include this range. Treating the factor as discrete numerical seems like a good option. Will treating it as continous during model fitting be fine in that case?
I'm not sure if this is a DOE any longer. I hope you can enlighten me. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
This study is a DOE.
The range 10-100 is included in the range of 0-500. So the model will be able to interpolate in the 'sweet spot' range even if the design does not include those particular levels.
I think it comes down to your beliefs about the restricted range of X1: 10-100. If you believe that
- the effect size is large relative to the the standard deviation of the response, say three times larger
- the minimum response occurs within this range
- the expected model is an adequate description over this range
If you believe all these claims are true, then use this range X1: 10-100 instead of X1: 0-500. Why complicate the study?
You are able to run a relatively large number of runs to study just two factors. (What about all of the other factors of this response? Keeping them constant? No chance of an interaction effect with them and X1 or X2?) So make a custom I-optimal design for a second order model with X1 and X2 with something like 20 runs. It will out perform the Box-Wilson design (central composite design) and the Box-Behnken design with regard to the data modeling. Here is a design candidate:
Notice that
- replication is a natural result of the larger number of runs
- there are generally three levels for each factor to support the second order model
- a couple of runs set X1 near but off center
- these odd runs increase the optimality
- these odd runs complicate the design (when you run it)
- feel free to change them to the center level with a very small loss in optimality
How well does this design perform?
The power is reasonably high if the effect size is at least twice as large as the response standard deviation. This result is a benefit of including 14 runs above the minimum number of runs. You want to use this model to determine the optimum factor settings that will minimize the response.
The variance of your model predictions will be quite low over a large interval of factor levels that is centered in the design space.
So I would drop the distinction about different levels for X1. That distinction comes from a design-centric or testing mindset. A study should come from a model-centric or experimenting mindset.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help on a continuous factor values/range for a DOE
Too just pile onto the already sage advice from my colleagues Mark, Ian, and Mike, if you are running JMP version 13 you may want to consider using the Compare Designs platform to evaluate how each of your candidate designs will perform from the perspectives shared by Mark in his post above.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us