- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Help me make sense of the significance in Chi-Square Analyses results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Help me make sense of the significance in Chi-Square Analyses results
Hey all,
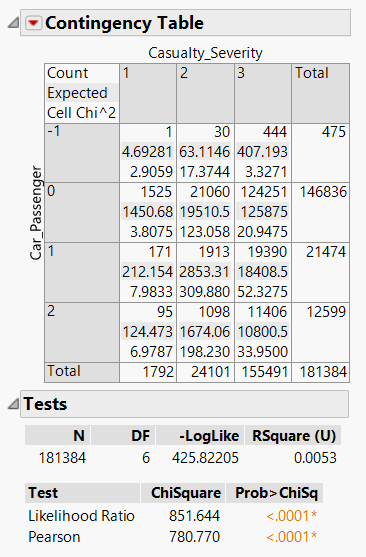
Here I have run the presense of a car passenger (1 = front seat, 2=back seat) against casualty severity (1 = fatal, 2 = serious, 3 = slight).
I am having trouble understand the results. I understand that the expected count and the actual count is what I'm interested in, but how do I detect whether the difference between those two counts is significant.
Thanks in advance!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help me make sense of the significance in Chi-Square Analyses results
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help me make sense of the significance in Chi-Square Analyses results
If there is no association, then the marginal distribution holds regardless of the level of the predictor variable. This quantity is provided by the column totals (count) at the bottom of the contingency table. The Expected value is based on the marginal distribution. So the Expected value for the first cell for Severity=1 and Car Passenger=-1 is 475*(1792/181384) and so on. The observed count is compared to the value expected if there is no association using a chi square distance: (Count-Expected)^2 / Expected. The chi square for the first cell is (1-4.69281)^2 / 4.69281 = 2.9059. The square root of the cell chi square is the Pearson residual and gives you an idea of the levels that are most important to the alternative hypothesis. Finally, you add all the cell statistics to obtain the sample chi square (labelled as Pearson in the bottom table). The sample statistic follows a chi square distribution under the null hypothesis and a large sample. The expected value is the degrees of freedom = (n row - 1)(n col - 1) = (4-1)(3-1) = 6. Your sample statistic 780.77 is much larger than 6 indicating strong evidence against the null hypothesis.
Your sample is very large so it is possible to detect weak associations. While the evidence strongly suggests the alternative hypothesis (there is an association), the R square value 0.0053 indicates that this association does not provide much predictive information. The odds ratio would indicate the strength of the association.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help me make sense of the significance in Chi-Square Analyses results
Mr.Bailey,
"Your sample is very large so it is possible to detect weak associations. While the evidence strongly suggests the alternative hypothesis (there is an association), the R square value 0.0053 indicates that this association does not provide much predictive information. The odds ratio would indicate the strength of the association."
Ok, awesome. The odds ratio you mention, is that the ratio between the expected and the observed?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help me make sense of the significance in Chi-Square Analyses results
No, an odds ratio represents the strength of the association, not the significance (chi square sample statistic), so it is the ratio of the odds of an outcome for different levels of the predictor or explanatory variable. For example, you might ask what is the odds ratio for Severity = 3 when Passenger = 0 versus Passenger = 2.
You need to use Analyze > Fit Model in order Use Ordinal Logistic platform to fit the logistic regression model. Then save the probability formulas that can then be used to compute the odds and the desired odds ratios.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us