- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
Hi everyone,
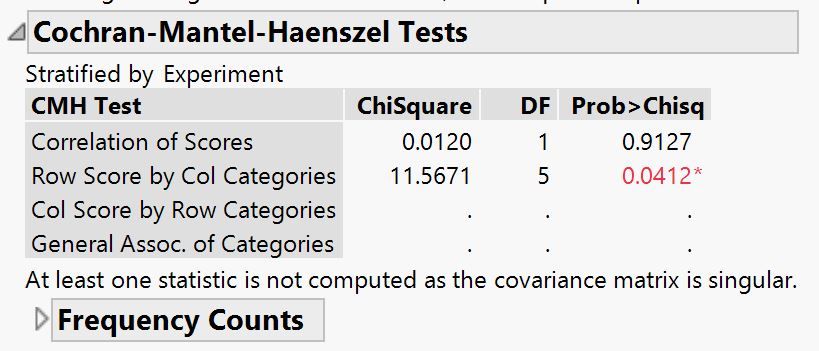
I'm conducting a Freidman test on a dataset. The data tests the effects of a treatment and consists of 10 subjects. Each subject had their heart rate (HR) measured six times over a period of 6 hours. To conduct the test, I saved the HR ranks (ordinal) and set is as the Y in the fit Y by X, the subjects as the 'Block', and the 'Hour' as the X. This is the output of the Cochran-Mantel-Haenszel Tests but I'm having difficulty interpreting them. Is there a significant effect eventhough the Correlation of Scores is much greater than 0.05? Also, if the results do show there are significant changes induced by the treatement, is it appropriate to conduct a Steel-Dwass all pairs test on the nominal data as a post hoc test?
Thank you for your help!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
I suggest trying the repeated measures analysis. Make sure that your data is organized as Heart Rate, Treatment, Subject, and Hour. See the A Multivariate Approach example in sample I cited.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
I see why the ranks work. I have never approached the non-parametric analysis this way.You were following the instructions correctly.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
The Contingency platform performs a cross-tabulation analysis. The analysis is based on counts, not ranks. The CMH tests introduce a stratification variable. The four versions of CMH depend on the modeling type of Y and X variables.
You should consider a repeated measures analysis instead. Please see this technical note for more information.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
Thanks for your reply. My data is nonparametric so that is why I was trying to conduct the Friedman test rather than the repeated measures analysis.
There were instructions that said to perform a CMH on ranks for the Friedman test in jmp.
https://www.jmp.com/support/help/14/nonparametric-multiple-comparisons.shtml
If this is incorrect, is there a way that I can still conduct the test?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
Data is neither parametric nor non-parametric. Data is continuous (measurement) or categorical (nominal or ordinal count). The analysis is either parametric or non-parametric.
Why did you decide to use a non-parametric analysis?
If you decide to continue with the non-parametric analysis, then know that JMP computes the ranks from your data. Do not compute the ranks beforehand and substitute ranks for the data.
The page that you cited is about non-parametric multiple comparisons. Is that what you need?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
I decided to do a nonparametric test because application of the Shapiro-Wilk test suggested my data is not normally distributed.
I have done the repeated measures but I am concerned that since my data might not meet the assumption of normality there is an increased chance of type 1 errors.
The page I cited says that the Friedman test is the nonparametric version of the repeated measures and that I should "Calculate the ranks within each block. Define this new column to have an ordinal modeling type. Enter the ranks as Y in the Fit Y by X platform. Enter one of the effects as a blocking variable. Obtain Cochran-Mantel-Haenszel statistics."
So I shouldn't calculate the ranks beforehand and just use the continuous rather than ordinal variable?
Thanks for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
The data are not assumed to be normally distributed in regression analysis. Do you mean that the residuals (estimated errors) are not normally distributed?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
Thank you for confirming that the analysis instructions were correct. So if my approach was correct, is there a significant effect even though the Correlation of Scores is much greater than 0.05? (as I originally asked)
Thank you again for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
Most statisticians I know don't take the Shapiro-Wilk test too seriously since it can be ridiculously over-sensitive, especially for large sample sizes. A lot of things that fail Shapiro-Wilk are normal enough to work well with parametric methods that assume normality. I always recommend looking at the normal quantile plot and using good judgement.
Additionally, you must absolutely check normality on residuals. If you have any effects in your data, the whole lump of data is probably not going to look normal. The assumption is around the errors, not the raw data values. Imagine if your model is 2 groups where there is a large group effect. Each group may be normally distributed, but the whole data set will look bi-modal.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help interpreting Freidman Test results (Cochran-Mantel-Haenszel)
The residuals do not provide a better estimate of normality. They provide a more relevant assessment.
The response (Heart Rate) is modeled as a combination of fixed effects (Treatment, Time) and random effects (Subjects, errors). Ordinary least squares regression uses a linear predictor for the fixed effects (response mean) and the normal distribution for the random effects (response variance). The response is the modeled as the combination so the data cannot be used to assess normality of the random part. The fixed effects must first be removed. The residuals are the observed response (combination) minus the mean response (fixed effects) for each observation. The remainder (residual) should be the random part. Save the residuals and examine their distribution before you decide that you need a non-parametric analysis.
Also, many times when the residuals are not normal a transform of Y can make them normal. This technique allows you to use the repeated measures analysis in a broader class of experiments.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us