- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Help Interpreting KSL test results in Goodness of Fit
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Help Interpreting KSL test results in Goodness of Fit
nHi All,
I'm looking at some goodness of fit results. While the Shapiro-Wilkes results have some (sparse) documentation, the Komologorov-Smirnov-Lilliefors test seems to have a different form and no documentation. A quick search shows nothing on the forum either; and google is quite quiet on the subject.
My results are:
For a Normal Distribution:
D Prob > D
0.3752777 < 0.0100*
I do not believe that this is a normal distribution. Can I reject the Null Hypothesis as D > alpha?
Why is Prob > D significant - does this just mean the test result is not likely as a random occurence?
For the LogNormal Distribution.
D Prob > D
0.030143 < 0.0100*
This is close to a Log Normal Distribution - it is mostly within the limits on the Normal quantile plot but wanders a little at the ends. As D is now less than alpha; does this mean that it fits a log Normal distribution?
FYI, There are ~159k data points.
The best link I can find on the subject is http://homepages.cae.wisc.edu/’1e642/content/Techniq ues/KS-Test.htm, which is what I am basing my assumptions on.
Thanks for any further information you can provide,
Gareth
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
The details and formulas of this test can be found on the following page: http://support.sas.com/documentation/cdl/en/procstat/63104/HTML/default/viewer.htm#procstat_univaria...
The null hypothesis for the KSL test is that the data are distributed as whatever distribution you have fit. Suppose you fit a normal distribution. Then the null hypothesis is that the data are normally distributed.
In order to interpret the test, the user must decide on an alpha level. Suppose you pick an alpha value of .05.
Receiving a p-value of 0.1500 indicates that one cannot reject the null hypothesis (because we chose an alpha of .05 which is less than the p-value).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
I have similar questions and it seems there is very little resource on this topic.
1. How does JMP calculate and report the KSL Test results?
2. How to interpret the D and Prob>D values reported by JMP?
3. Does user have control over the Alpha / Significant Level? If yes, how?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
The details and formulas of this test can be found on the following page: http://support.sas.com/documentation/cdl/en/procstat/63104/HTML/default/viewer.htm#procstat_univaria...
The null hypothesis for the KSL test is that the data are distributed as whatever distribution you have fit. Suppose you fit a normal distribution. Then the null hypothesis is that the data are normally distributed.
In order to interpret the test, the user must decide on an alpha level. Suppose you pick an alpha value of .05.
Receiving a p-value of 0.1500 indicates that one cannot reject the null hypothesis (because we chose an alpha of .05 which is less than the p-value).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
with this size of sample size everything comes out as significant (for good or bad). this is since every little difference is "detectable". with this sample i would first mach things visually.
I also find the p values of this test rather suspiciously rounded. if you just omit some observations and repeat the test it will still give the exact same p value.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
You are correct about the sample size/significance issue.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
You are correct about the sample size/significance issue.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
Thank you for the pointers.
While a sample size of ~159k is considered as large and highly detectable in the context of rejecting the null hypothesis, is there a number where we consider a sample size as "large and highly detectable"? And if this number is based on a theory, or a general rule of thumb? In my case, I could be working on a sample size of ~40k.
To add, my intention is to attempt to avoid visual inspection of the histograms. I could be dealing with ~40k of units in a particular product, where each unit is taken ~3000 different kinds of measurements. Assuming we expect every single kind of measurement to produce a Normal distribution behaviour. I imagine, if possible, I could run the Normality test using JMP to report the p-value for each of the 3000 measurements. By looking at 3000 p-values as the first gross screen, it allows me to quickly identify problematic measurements (that are not Normal) instead of viewing through 3000 histograms manually. For this, we need (1) accuracy and robustness from the Normality test, and (2) automation in JSL supported to report these p-values. If there's any advice on such usage model, that'd be very much appreciated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Help Interpreting KSL test results in Goodness of Fit
in this case you may want to try the following steps:
1) open your data table.
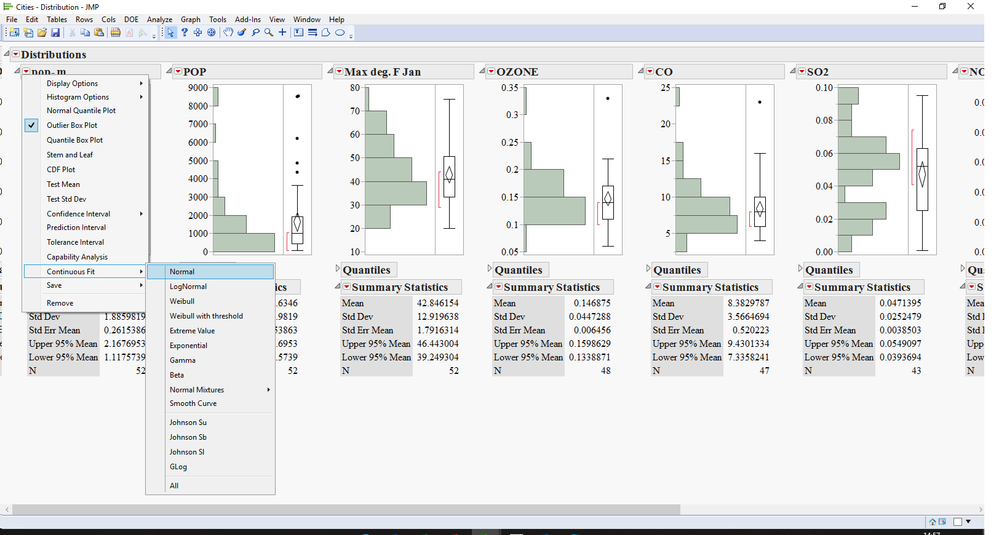
2) run a distribution with all the variables you want.
3) hold the Ctrl key and fit the normal distribution to all variables
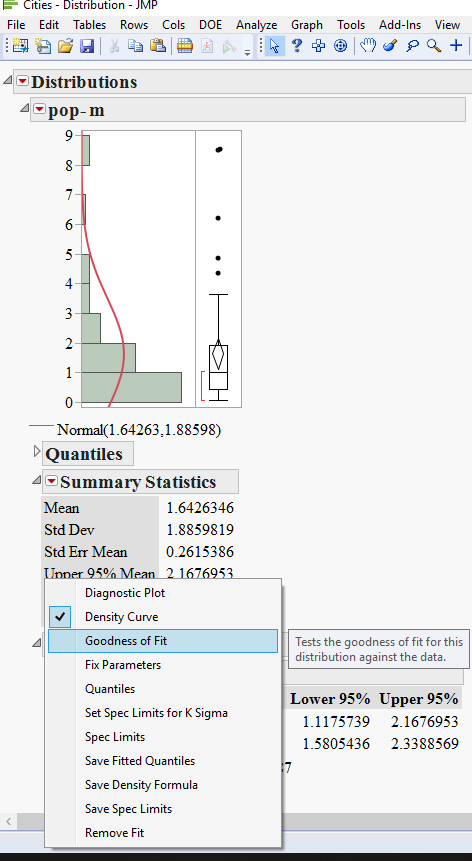
4) hold the Ctrl key and get the goodness of fit
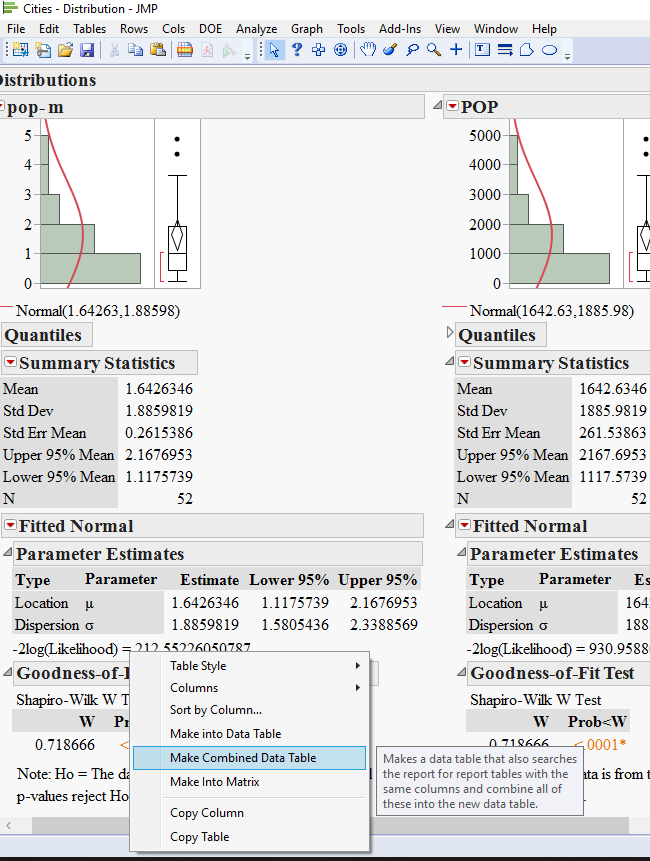
5) now comes the trick: right click on one of the goodness of fit tables and choose Make combined data table.
now you should have a fully functional table with all your results at once. this will allow you to sort by the statistic value or Pvalue or even make a graph of what you just got.
hope this helps.
ron
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us