- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Getting calculated control limits from a Levey Jennings chart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Getting calculated control limits from a Levey Jennings chart
Hi Everyone,
I'm currently working on a script that generates a LJ chart. I need to drop a bunch of lines in there and must make sure the scale of the Y-axis allows to see all these lines.
This all works perfectly except for the calculated control limits. Is there any way that I can get these calculated limits, preferably before I generated the chart, so I can use them in the calculation I make to determine the Y-axis scale?
Thanks!
--Jan
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Getting calculated control limits from a Levey Jennings chart
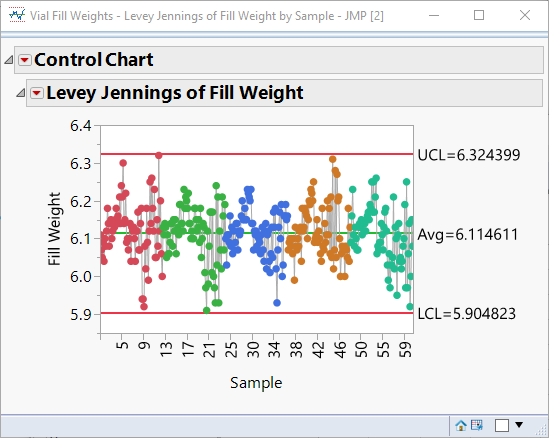
Levey Jennings just uses the long term sigma to compute control limits, so you can just take the standard deviation of the entire column of the response you are plotting. Here's an example using the Vial Fill Weights example from the Sample Data Library.
dt = Data Table("Vial Fill Weights");
y = :Fill Weight << Get Values;
y_bar = mean(y);
sigma = std dev(y);
UCL = y_bar + 3*sigma;
LCL = y_bar - 3*sigma;This returns 5.90482338181099 and 6.32439884041124 for LCL and UCL respectively. This matches the Levey Jennings limits:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Getting calculated control limits from a Levey Jennings chart
Levey Jennings just uses the long term sigma to compute control limits, so you can just take the standard deviation of the entire column of the response you are plotting. Here's an example using the Vial Fill Weights example from the Sample Data Library.
dt = Data Table("Vial Fill Weights");
y = :Fill Weight << Get Values;
y_bar = mean(y);
sigma = std dev(y);
UCL = y_bar + 3*sigma;
LCL = y_bar - 3*sigma;This returns 5.90482338181099 and 6.32439884041124 for LCL and UCL respectively. This matches the Levey Jennings limits:
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us