- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Fractional Factorial - Understanding Aliasing Matrix
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Fractional Factorial - Understanding Aliasing Matrix
Hi all,
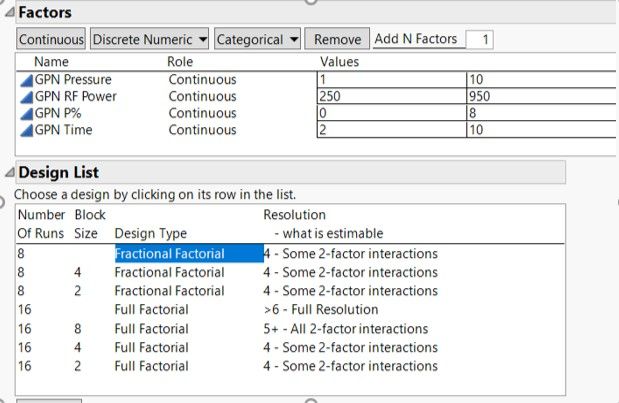
I would like to design a fractional factorial design. There are 4 factors.
I could afford only max 12 run, including 4 center points.
The highlighted 8 runs with resolution 4 is chosen.
Now, come to the question.
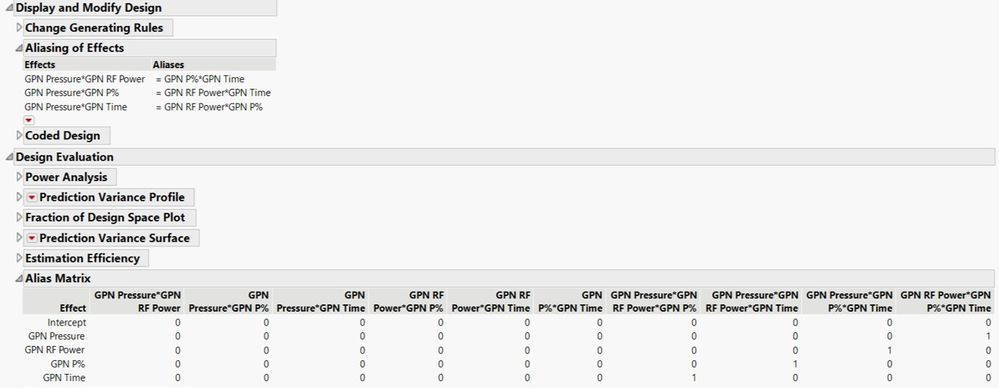
In terms of aliasing, the factor "GPN time" is known to have less significant impact. Therefore, the factor "GPN time" is afford to be aliased.
Above is the aliasing of effects generated by JMP.
How to read the alias matrix? Can someone please explain in simple term?
Is the factor "GPN time" aliased correctly?
Thank you in advance.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fractional Factorial - Understanding Aliasing Matrix
In a resolution IV design main effects are not aliased with each other, nor with two-factor interactions. There will however, be aliasing between two-factor interactions. That is the aliasing being shown in the tabulation for "aliasing of effects". For example, it is showing that GPN Pressure * GPN RF Power is aliased with GPN P% * GPN Time. If you want you can click the red triangle and it will show you, for each term, what the aliasing pattern is (if any).
Based on this aliasing you would not expect to see any correlation between the estimates of the main factors and two-factor interactions, and that is confirmed by the alias matrix. Zero indicates no correlation (because there is no aliasing). The 1's that are appearing in the matrix relate to three-factor interactions. If you click the red triangle under aliasing of effects it will also show you that all main effects are aliased with three-factor interactions. As a general rule we worry about anything beyond 2nd order effects.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fractional Factorial - Understanding Aliasing Matrix
In a resolution IV design main effects are not aliased with each other, nor with two-factor interactions. There will however, be aliasing between two-factor interactions. That is the aliasing being shown in the tabulation for "aliasing of effects". For example, it is showing that GPN Pressure * GPN RF Power is aliased with GPN P% * GPN Time. If you want you can click the red triangle and it will show you, for each term, what the aliasing pattern is (if any).
Based on this aliasing you would not expect to see any correlation between the estimates of the main factors and two-factor interactions, and that is confirmed by the alias matrix. Zero indicates no correlation (because there is no aliasing). The 1's that are appearing in the matrix relate to three-factor interactions. If you click the red triangle under aliasing of effects it will also show you that all main effects are aliased with three-factor interactions. As a general rule we worry about anything beyond 2nd order effects.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fractional Factorial - Understanding Aliasing Matrix
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fractional Factorial - Understanding Aliasing Matrix
Thanks for the spot @statman. Yes that is what I meant!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us