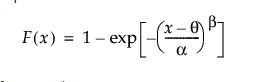- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Formula for Weibull distribution with a co-variate
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Formula for Weibull distribution with a co-variate
Hello,
I performed a survival analysis with censored data, and a co-variate called "AGE". I used "Save Probabilty Formula" to save the formula in the data table. Now when I right click the newly created column, and click on "Formula", I get the below formula.
My question is could someone advise on the actual formula for Weibull Distribution where I can substitute the calibrated co-efficients, and input parameters to calculate the outputs?
I searched around on the JMP website and found the below formula for Weibull distribution:
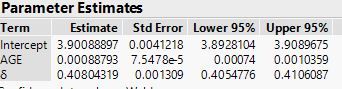
But I am not clear which co-efficient goes where, and what to do with the additional co-efficient of the co-variate "AGE". Below are the estimated parameters calibrated by JMP.
I apologize, I am an engineer and I am not very stat-saavy.
Thank you,
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for Weibull distribution with a co-variate
I am not clear why you can't use the column formula to "calculate output."
There are two popular parameterizations of the Weibull model. JMP uses the location and scale version because it has better numerical properties when estimating the parameters. The more commonly used parameterization, though, is the shape and scale version. The formula you found is the latter version. It is easy to convert between them. In fact, the column formula has already done it for you.
The scale parameter alpha is equal to the reciprocal delta, so JMP's function shows the second argument as 1 / 0.4080431942. The shape parameter beta is equal to the log of mu, so JMP's function shows the third argument as e^(3.9008889732 + 0.0008879281 * Age). The shape parameter is a function of Age, while the scale parameter is independent of Age.
LOWERDELTA appears to be the quantile you used as a response. F(x) is the cumulative distribution function. It returns the probability of obtaining a value between 0 and the given quantile.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Formula for Weibull distribution with a co-variate
Hi Mark,
Thanks for the reply.
The reason why I want to know the formula and sort of "plugin" the parameters to evaluate the risk is I am trying to prepare a report by reporting the formula and associated parameters. So any one who is reading the report, irrespective of owning JMP, could "plugin" the parameters and the quantile to evaluate the risk.
Essentially, I will have to report the formula, and tabulate the respective parameters, which should enable the readers to evaluate risk for their chosen quantile (s).
Hope that makes sense.
Thanks,
Mike
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us