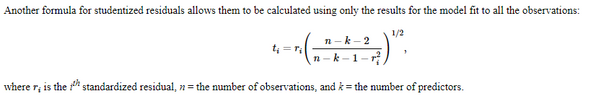Formula behind externally Studentized Residuals

[#1]

I am trying to calculate the externally studentized residuals (jackknife residuals if you like) manually i.e. replicate the results that is already available from the "Save Columns" menu in the "Fit Least Sqaures" platform. 

The documentation for JMP 17 doesn't list which formula is used behind the scenes, but the assumption is that it would follow literature, such as ch7.pdf (jhsph.edu) (also see attached screenshot from chapter to get context). The online documentation (https://www.jmp.com/support/help/en/17.0/#page/jmp/row-diagnostics.shtml#ww694286) wrongly states that one can only save the Studentized residuals, not the externally Studentized - this could need revision. 

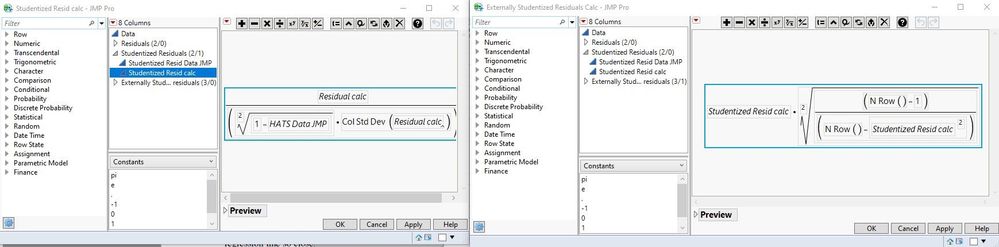
I have been trying the "easy" way from above, but I cannot arrive at the exact same result as JMP - depending on the dataset I can get within 4-5 decimal accuracy, but on others result differ already on the first digit, which worries me. Can someone elaborate on how JMP calculates the externally Studentized residuals? I have put together a simple dataset and added a regression model that can be used to extract residuals (no fixed factors i.e. p=0). The above formula requires the extraction of HATS as well, so these are also saved as a column (I can calculate these manually though). As the file shows everything matches fine when calculating residuals and internally Studentized residuals, but I cannot get the externally Studentized residuals to match

Formulas in columns:

A side note: Could it be considered to allow JMP to save the limits for the Studentized residuals as well? These I can calculate manually, but it is a hassle to keep track of factors and degrees of freedom manually. I would be great to be able to save these limits as a column.

[#2 · Accepted solution]

Looks like JMP uses the formula here, which is slightly different than yours, and for smaller sample sizes can be markedly different.

https://online.stat.psu.edu/stat462/node/247/

[#3]

While posting the above, several of my colleagues argued back and forth and a suggestion was made to consider n the jackknifed count and not the total row count so n was in fact n-1. A bit embarrassing this solves the problem altogether as the numerator in the last formula then becomes N Row()-2 and the denominator becomes N Row()-1-Stud.Res.Calc^2.

Instead of deleting this post I will let it remain for others who might need to calculate these residuals manually. 

Edit: I see this confirms the above reply, which I gratefully accept as the solution. Thank you.

[#4]

Glad to help...I noticed further, that the formulas are actually the same. In yours, p = number of parameters (p=1 since you are estimating the intercept). In the reference I provided, k=0 since k is the number of predictors. So, if you substitute  p=k+1 in your reference the result is the same as my reference. 

[#5]

Exactly. I could probably have saved myself the trouble of writing a post, if I had created my formula with p included as a table variable, as I would most likely have hit p=1 by accident when testing the formula. Usually, I would not count the intercept as a predictor but that one is on me.