- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Fischer's exact test odds ratio and Confidence intervals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Fischer's exact test odds ratio and Confidence intervals
Hi,
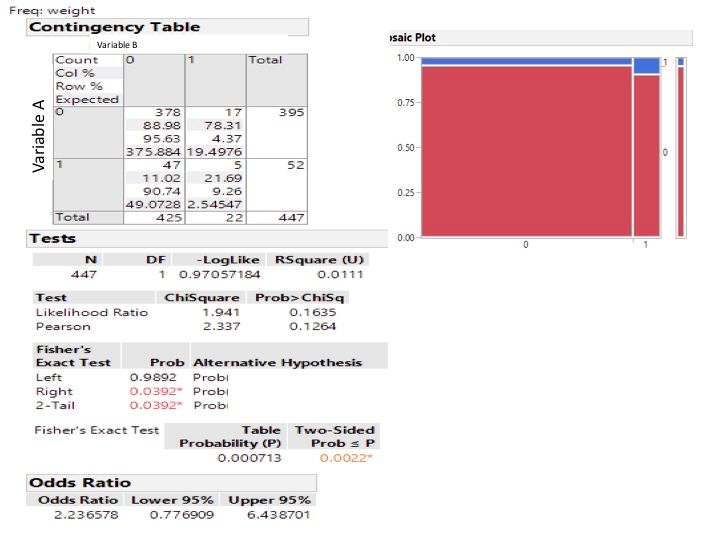
I am a regular user of JMP, but without experience in scripting. I have used Fischer's exact test on my analysis, and am getting the results as posted. I have 2 questions:
1. Why do I get 2 difference exact tests and p-values? Which is the one to use?
2. In the odds ratio, the confidence interval does not match the p-value (which is <0.05). I am guessing it has something to do with the way with the CIs are calculated. Can you advise the best way to calculate the exact CI here? I am not experiencing this issue with other exact analyses used in the same dataset
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
- You do not understand the exact test for a 2x2 contingency table. It is possible to use it three ways. The Alternative Hypothesis explains each way and allows you to decide which of the three tests is appropriate for your decision.
- The odds ratio confidence interval does match the tests. The p-values are greater than alpha = 0.05 and the 95% confidence interval for the odds ratio includes 1.
I have no idea what you might have done wrong or differently with this analysis compared to other analyses with the same data set. What other analysis is there?
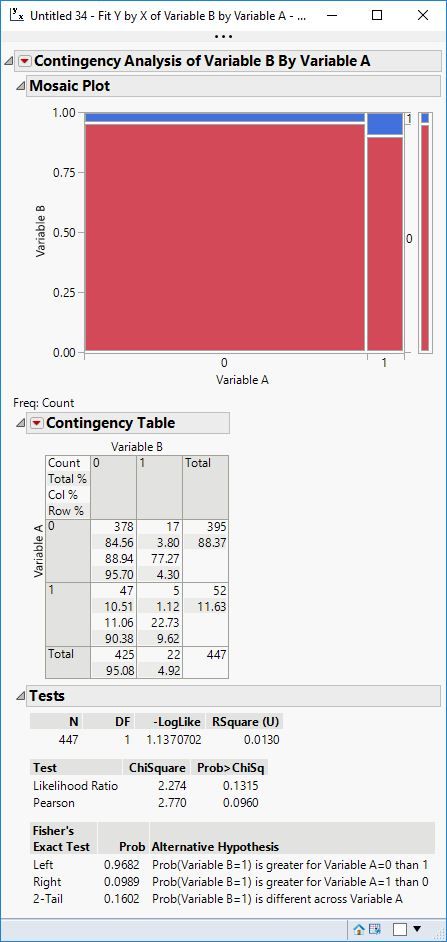
I do not get the same result for the analysis of the same data. See my result:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
It looks like the first analysis used the Weight for the Frequency while you used the Counts; would that be a possible source of different behavior?
Best,
TS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
Thanks for your replies. I also think the 'weight' (which is a sampling weight for the study design) may have changed things, as @Thierry_S suggests. If I only use the 'counts' from this 2*2 table in the 'frequency' section of the contingency platform, I am getting the same results as you, @Mark_Bailey . As for the alternative hypothesis, I would need to use the one that corresponds with two-tailed values only
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
Why are weights for non-responders used? How are the weights determined?
Using the weight role will change the result of the analysis.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
This was a survey with ~50% response rate with differences between responders and non-responders, thus our decision to adjust for non-response. Weights were calculated on the basis of 3 baseline characteristics that affected response. Weight calculation was done as follows: for each combination of the 3 variables, the total number with that combination in the original cohort and was divided by the number of patients with that combination who completed a survey.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
How do you know "differences between responders and non-responders" if the non-responders did not respond? I better let someone who is more familiar with this kind of analysis take over!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Fischer's exact test odds ratio and Confidence intervals
Hello @Mark_Bailey . I was wondering if you had any additional insights to this. I haven't found a solution to this problem yet.
I tried making contingency tables (with the numbers I get after weighting)- this seems to give me OR and 2-tailed p-value for the exact test which are consistent with each other. I ran these for several analyses, which seem to give similar but not exactly the same results compared to when the weighting variable is used.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us