- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Failed to converge(step halving limit). Solution for this error?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Failed to converge(step halving limit). Solution for this error?
I have 3 continuous factors and one of the outcome of the study was if product pass or fail (data is attached), when I try to run ordinal logistic for this I get an error 'ALERT:FAILED TO CONVERGE(STEP-HALVING LIMIT)' and after the alert it gives me an output but not sure if the results are reliable or not. Why am I getting this error and how to fix this?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failed to converge(step halving limit). Solution for this error?
I don’t have JMP at the moment. Do you have a separation problem? Did you select the Firth bias adjustment option in the Fit Model dialog?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failed to converge(step halving limit). Solution for this error?
@Mark_Bailey I think this is separation problem (I was reading few articles and I think its separation problem). No I did not select Firth bias adjustment option in the Fit Model dialog
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failed to converge(step halving limit). Solution for this error?
The firth bias adjustment isn't available anymore as an option in Fit Model.
I also noticed the "defect" variable is specified as Ordinal. Change it to be Nominal. It at least won't give you the step-halving error in Fit Model, and then the output will tell you that all the parameter estimates are unstable (indicating separation).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failed to converge(step halving limit). Solution for this error?
Oh wait, the Firth bias adjustment is available if you choose Generalized Linear Model as the Personality in Fit Model, but then you have to specify the distribution (Binomial) and the link function (logit).
I still think the ridge estimation method in Generalized Regression is better though, for this situation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failed to converge(step halving limit). Solution for this error?
My mistake! I was thinking 'logistic regression' but it is not the Nominal Logistic or Ordinal Logistic personality. It is the Generalized Linear Model personality. It offers the Firth bias adjustment with a binary response.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failed to converge(step halving limit). Solution for this error?
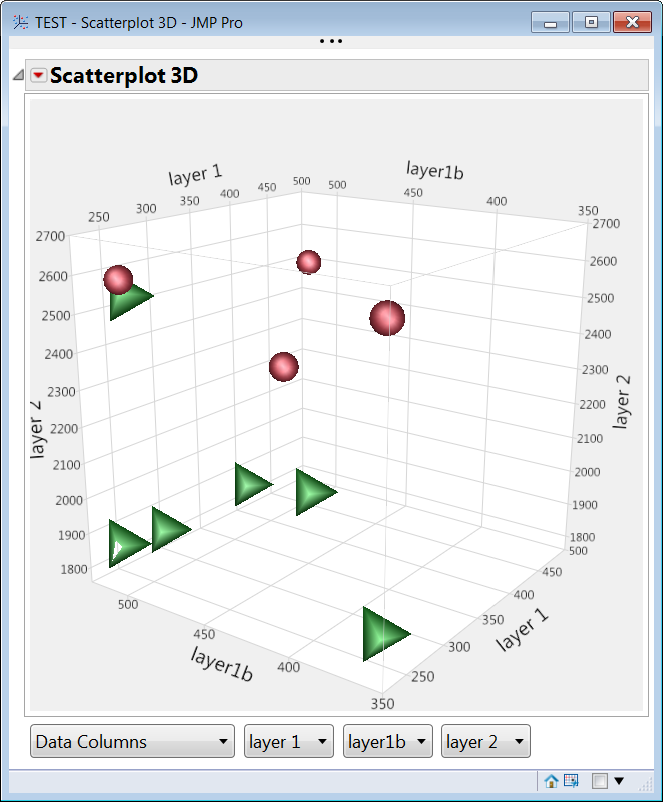
I think the problem is that you have "perfect separation" in the data. See the 3D scatterplot of the 3 factors, color/marked by Pass/Fail (pass is green pyramid, fail is red circle). You can draw a plane in that space that separates the pass/fail results. To do a logistic regression with out convergence errors, you need some overlap of passing and failing conditions in the factor space. If you do the fit in Generalized Regression with main effects only, you will see that one of the factor effects cannot be estimated.
It is a bit curious that when you do the logistic regression fit with the main effects + two factor interactions in Generalized Regression, you don't get the error (it must be doing some parameter regularization?), but for that fit you see that all of the main affects are not significant but the two factor interactions are all significant. That is also very unusual, indicating the model is over specified. Also the confidence intervals for the parameter estimates are huge, also indicating the problem of separation.
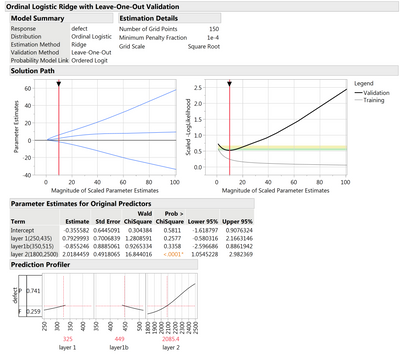
What you can try to do is fit the ordinal logistic regression model using the "Ridge" estimation method (which will do parameter shrinkage and help overcome some of the separation problems, and use leave-one-out as the validation method (used to choose the optimal ridging parameter). This gives a stable model fit, but you still need to check to see if this model makes sense.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Failed to converge(step halving limit). Solution for this error?
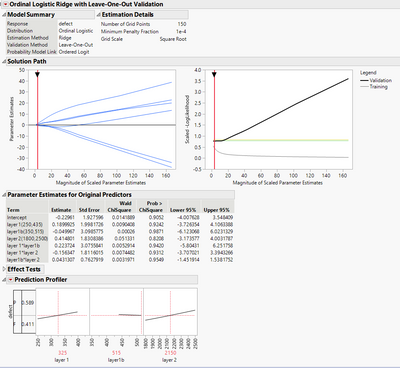
@MathStatChem Thank you for detailed response. The solution you mentioned gave the model that will work but when I tried to do it I am getting different results (In parameter etimates table I am not all the main effects as well as two way interactions listed and none of these are significant). Is there something I am missing here?
Also, as you mentioned if I change this variable from ordinal to nominal it changes distribution to 'multinomial' and gives back model with no significant results.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us