- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Estimating the most important features to each k-means clusters
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Estimating the most important features to each k-means clusters
Hi,
I use kmeans cluster to group data together. Now I want to find out for each cluster of data, which feature has high impact. I wonder if JMP pro K-mean provide estimation of most important features to each k-means clusters? Can someone provide suggestion how I can I calculate it if it is not available? I was thinking perhaps the distance can be used for estimation. Any though?
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Estimating the most important features to each k-means clusters
Hi @dadawasozo,
If I understand better your objective, you would like to better assess the disparities and differences between clusters based on the values of the features ?
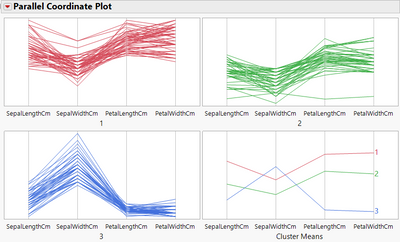
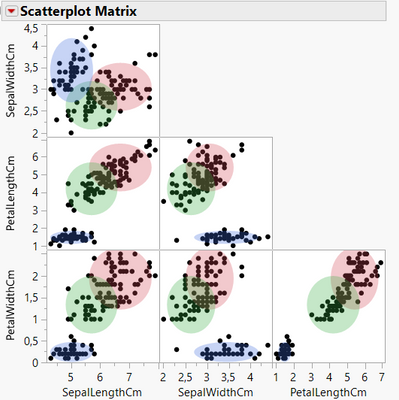
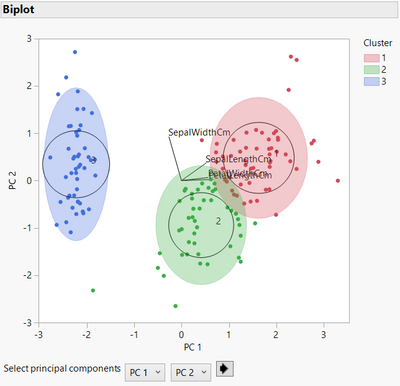
If yes, you can look at the options "Parallel Coordinate Plot", "Scatterplot matrix" and the several graphs "Biplot" available in the red triangle next to "KMeans NCluster = (X)", as they provide, with the summary statistics "Cluster Means", interesting visualizations on how the several clusters differ based on the features mean values.
Example Parallel Coordinate Plot on Iris dataset (you can reproduce it with the Graph Builder to customize it and add values legends):
Example Scatterplot matrix on Iris dataset :
Example Biplot 2D (with Principal Components) on Iris dataset :
I hope I understand better your objective and that this answer may help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Estimating the most important features to each k-means clusters
Hi @dadawasozo,
I think about two possible ways to explain the clustering done with K-means :
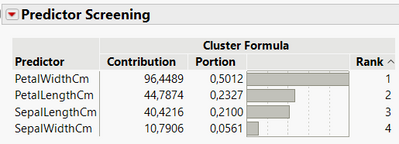
- You can use the cluster formula as a response, and try to model this cluster response based on your inputs. One flexible and efficient plaftorm to do this may be the Bootstrap Forest (JMP Pro) or Predictor Screening (JMP). You can then compare the contributions of your factors to the clustering.
- You can also think about this in a "statistical" way : the more importance a factor has on the clustering, the more separated are the points on this factor axis (it's easier to create clusters if you can separate/discriminate points based on one or several factors). So you can use the "Fit Y by X" platform, use the clusters as your X and your factors as the Y's, and compare the F ratios of the several fits using a parametric test (t-test, Welch, ...).
Depending on the adequate use of the statistical test and verification of assumptions (normality, variance equality, independence, no outliers, ...), you may find a similar result than the option 1.
As an example:
On the very famous and public "Iris" dataset, I did the K-means clustering on the factors Sepal length, sepal width, petal length and petal width. I am able to find three clusters, that match closely with the three species found. I save the cluster formula.
- When using the Predictor screening platform, entering the cluster formula as the Y, response and the factors as X's, I can have a look at the difference in contributions of my factors on the clustering :
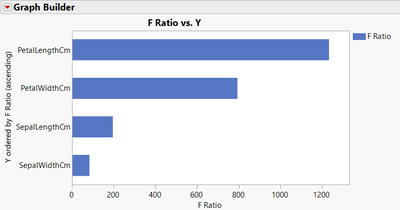
- When using the "Fit Y by X" platform, entering the cluster formula as X and the factors as Y's, I do a Welch's test and create a combined datatable with all F ratio. With a graph showing the F ratio depending on the factors, I'm able to find similar results :
There is a difference between the two platforms and an exchange between the two biggest clustering contributors factors, because petal length and petal width have both two non-normal distributions. Hence the Welch's test wouldn't be the most appropriate option here, but a Steel-Dwass All Pair test would be probably better.
On this dataset, the Predictor screening would be a safer option as it is robust against outliers, and does not require assumtions about the data distributions (the platform uses a Random Forest model).
I attached the Iris datatable so that you can look at the several analysis and reproduce the tests I have done.
Last aspect to take into consideration (even if out-of-scope of your question) is to make sure that K-Means approach is suitable for your dataset as it is based on two assumptions :
- Clusters are spherical (all variables have the same variance),
- Clusters have similar size (roughly equal number of observations in each cluster).
Other clustering approaches may be more flexible if these assumptions are not met (Gaussian/Normal Mixtures for example), or more "appropriate" depending on your clustering context : clustering based on points density, based on assumed underlying distributions, on hierarchical relations between points, ...
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Estimating the most important features to each k-means clusters
Hi Victor,
is it possible to get the most important features for each cluster separately? K means helps clusters data into few groups. I want to understand the most impactful features for each cluster to understand what makes them different clusters.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Estimating the most important features to each k-means clusters
Hi @dadawasozo,
If I understand better your objective, you would like to better assess the disparities and differences between clusters based on the values of the features ?
If yes, you can look at the options "Parallel Coordinate Plot", "Scatterplot matrix" and the several graphs "Biplot" available in the red triangle next to "KMeans NCluster = (X)", as they provide, with the summary statistics "Cluster Means", interesting visualizations on how the several clusters differ based on the features mean values.
Example Parallel Coordinate Plot on Iris dataset (you can reproduce it with the Graph Builder to customize it and add values legends):
Example Scatterplot matrix on Iris dataset :
Example Biplot 2D (with Principal Components) on Iris dataset :
I hope I understand better your objective and that this answer may help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us