Estimating slopes and intercepts in ANCOVA

[#1]

I am feeling particularly dumb today and hope someone can help me feel smarter.  When running an ANCOVA with separate slopes, I would like to get estimates of the slopes and intercepts of each group along with the t-tests of significance.  In SAS, I can run GLM and specify the model like this (using the JMP "Drug" data table):

model y = Drug Drug*x / noint solution;

I cannot find anything in JMP that is comparable to this.  Specifying the same model above in the Fit Model dialog gives me something totally unlike what SAS gives.  I have tried displaying indicator parameter estimates, extended estimates, and pretty much everything this is under the "Effects" menu item in the Fit Model results window.  I realize that JMP parameterizes the model differently than SAS, but I have not yet found the correct combination of model specification and options to duplicate the SAS results.  I also realize that one can figure out what the slopes and intercepts are from the parameter estimates table, but the tests are testing whether the deviations are significantly different from zero, not whether the group slopes and intercepts are different from zero (unless I am actually dumber than I feel today).

[#2]

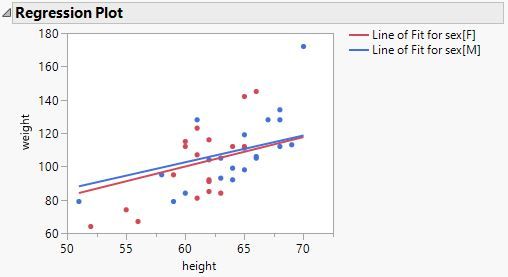
I just used the JMP example Big Class. I used Analyze > Fit Model to specify the model and then clicked the red triangle to select Submit to SAS. This program is what JMP created for me.

DATA Big_Class; INPUT  sex &$ height weight; Lines;
F  59  95  
F  61  123  
F  55  74  
F  66  145  
F  52  64  
M  60  84  
M  61  128  
M  51  79  
F  60  112  
F  61  107  
F  56  67  
M  65  98  
M  63  105  
M  58  95  
M  59  79  
F  61  81  
F  62  91  
F  65  142  
F  63  84  
F  62  85  
M  63  93  
M  64  99  
M  65  119  
M  64  92  
M  68  112  
M  64  99  
M  69  113  
F  62  92  
F  64  112  
M  67  128  
M  65  111  
M  66  105  
M  62  104  
M  66  106  
F  65  112  
F  60  115  
M  68  128  
F  62  116  
M  68  134  
M  70  172  
;
RUN;

PROC GLM  DATA=Big_Class ALPHA=0.05;
CLASS sex;
MODEL  weight =  sex height sex*height / noint solution;
RUN;

Here is the SAS output:

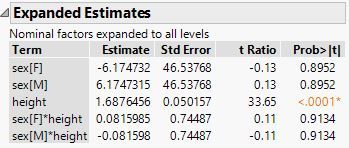
First of all, you requested a linear model without an intercept. Simply check this option in the middle of the bottom of the Fit Model launch dialog. Click the red triangle and deselect Center Polynomials. Click Run. Then click the red triangle at the top and select Estimates > Expanded Estimates.

Here is the JMP output:

The estimates are different because JMP parameterizes the terms differnently than PROC GLM. Is this report what you are looking for?

[#3]

Thanks for your quick reply.  Your example actually illustrates my point.  The intercept estimates from SAS do not match those from JMP, not even close.  The intercept estimates from JMP appear to be deviations from something, but it is not clear to me what that could be.  The situation becomes even more unclear if you run the model with the "height" main effect.

[#4]

There is no intercept parameter in either SAS or JMP model specification, so there is no estimate for the intercept. (Edit: I realize that you refer to the group effect as an intercept. That is a fair interpretation but different from my own. The interpretation of the intercept is murkier without centering, too.)

The effect test for the interaction is used to determine if the slope is different for any group. (Edit: I don't think I am clear about what you want. Discrepancies aside, the JMP output (what is provided) is the same as SAS.

I am looking into the nature of the differences between SAS GLM and JMP Fit Least Squares but I do not know when I might have an explanation.

[#5]

Using the BigClass data, this is what I get from PROC GLM with MODEL weight = sex sex*height / noint solution;

Parameter	Estimate	Standard Error	t-value	Pr > |t|
sex F	-189.7725451	65.19174041	-2.91	0.0061
sex M	-109.0144590	51.63743795	-2.11	0.0418
height*sex F	4.7745491	1.06889262	4.47	<.0001
height*sex M	3.4006530	0.80623574	4.22	0.0002

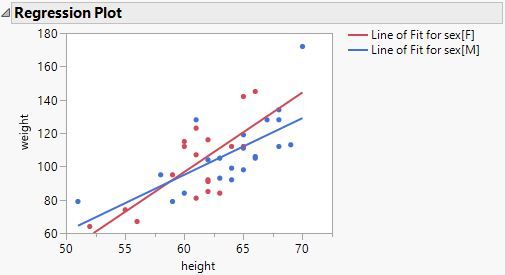
The interpretation of the two sex parameter estimates is that they are the intercepts for F and M and the height*sex parameter estimates are the F and M slopes.  The tests in this table are testing whether these parameter estimates are significantly different from zero.  My original question primarily concerned how to duplicate this table in JMP.  The graph produced by Fit Model is the same as the graph produced by PROC GLM, but the parameter estimates tables are very different.

[#6]

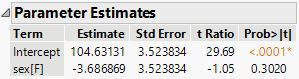
Trying to keep the comparison of like models, here is the SAS output for weight = sex with an intercept:

So the mean weight for sex = F is equal to 108.3181818 - 7.3737374 = 100.94444 (prediction).

Here is the JMP output for the same model:

So the mean weight for sex = F is equal to 104.63131 - 3.686869 = 100.94444, the same predicted value

Let's remove the intercept term from the model and see what happens. Here is the SAS output for the new model:

The mean weight for sex = F is 100.94444 again.

How about JMP?

Hmm, that's different. This estimate is not wrong, though! JMP uses effect coding for the linear predictor and this constrained model model is not the same as the constrained model in SAS GLM,. This estimate is the best in the least squares sense but it is not a good fit with only sex for the predictor. You should not remove the intercept. That is the lesson here.

[#7]

I did hear back from JMP Technical Support about the differences:

"In a simple case of the model weight=sex, PROC GLM includes a column in the design matrix for both levels of ‘sex’, so when the intercept is removed, there are still 2 columns left for the two parameters (one for male, one for female). JMP, on the other hand, will only have a single column in the design matrix, so only one parameter is estimated. They won’t match with no intercept models if categorical effects are included."

[#8]

This is the ANCOVA model that you fit (still using Big Class example):

This is the ANCOVA model of the same data with an intercept term and a centered continuous predictor:

The conditions of the first model are very different than those of the second model. They are not just mathematical alternatives (intercept and categorical effect versus categorical intercepts).