- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Efficient moving average algorithm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Efficient moving average algorithm
Hello,
Thanks to those who have posted on here before, I've found some useful answers!
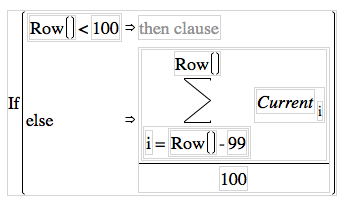
I have several large data sets (20 million points each!) from an oscilloscope. I want to calculate a moving average. However, the algorithm I've devised is very slow. Here is the code for my formula:
"
If(Row() < 100, Empty(), Summation(i = Row() - 99, Row(), :Current[i,Empty()]) / 100)
"
As the width of the averaging window (in this case 100 samples) gets larger (say 500, 1000, or even 50000 or more), the calculation time becomes unreasonable. Does someone have a faster way of doing a moving average?
Thanks!
Dane
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Efficient moving average algorithm
I can offer a couple of strategies here.
I think both are more efficient that the Summation() operator you're currently using. I can't say they are the most efficient possible though.
1) Use the Sum() function on a matrix.
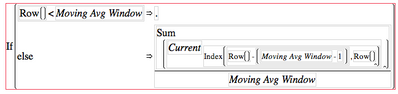
If(Row()<:Moving Avg Window,
.,
Sum( :Current[Index( Row() - (:Moving Avg Window - 1), Row() )] ) / :Moving Avg Window
)
This takes advantage of the speed of the matrix operation. The subscript of the Current column in this formula is a matrix of the row numbers from the start of the moving average window to the current row number. My subscripting the column this way JMP returns a matrix and the Sum function is relatively efficient over a matrix.
An even faster way though is to calculate this moving average over two columns. The first column simply maintains a moving sum by adding the value of Current in one row to the value of the rolling sum in the previous row and then subtracting the value of Current from the row at the beginning of the window.
Here's the formula for Moving Sum.
If(Row()<=:Moving Avg Window,
If( Row() == 1,
:Current,
Lag( :Name( "moving sum(x)" ), 1 ) + :Current
),
(Lag( :Name( "moving sum(x)" ), 1 ) + :Current) -
Lag( :Current, :Moving Avg Window )
)
Then it's easy to have a column that divides Moving Sum by the Moving Avg Window.
If(Row()>=:Moving Avg Window,
:Name( "moving sum(x)" ) / :Moving Avg Window,
.
)
I'm attaching a data table that shows both of these methods. In the data table the Moving Avg Window is a Data Table Variable.
To see the efficiency of the second method in this data table you may want to suppress the evaluation of the of the Moving Avg(x) column first.
-Jeff
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Efficient moving average algorithm
I can offer a couple of strategies here.
I think both are more efficient that the Summation() operator you're currently using. I can't say they are the most efficient possible though.
1) Use the Sum() function on a matrix.
If(Row()<:Moving Avg Window,
.,
Sum( :Current[Index( Row() - (:Moving Avg Window - 1), Row() )] ) / :Moving Avg Window
)
This takes advantage of the speed of the matrix operation. The subscript of the Current column in this formula is a matrix of the row numbers from the start of the moving average window to the current row number. My subscripting the column this way JMP returns a matrix and the Sum function is relatively efficient over a matrix.
An even faster way though is to calculate this moving average over two columns. The first column simply maintains a moving sum by adding the value of Current in one row to the value of the rolling sum in the previous row and then subtracting the value of Current from the row at the beginning of the window.
Here's the formula for Moving Sum.
If(Row()<=:Moving Avg Window,
If( Row() == 1,
:Current,
Lag( :Name( "moving sum(x)" ), 1 ) + :Current
),
(Lag( :Name( "moving sum(x)" ), 1 ) + :Current) -
Lag( :Current, :Moving Avg Window )
)
Then it's easy to have a column that divides Moving Sum by the Moving Avg Window.
If(Row()>=:Moving Avg Window,
:Name( "moving sum(x)" ) / :Moving Avg Window,
.
)
I'm attaching a data table that shows both of these methods. In the data table the Moving Avg Window is a Data Table Variable.
To see the efficiency of the second method in this data table you may want to suppress the evaluation of the of the Moving Avg(x) column first.
-Jeff
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Efficient moving average algorithm
Thanks, Jeff. These run much faster than the summation method!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Efficient moving average algorithm
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Efficient moving average algorithm
I usually find that if I can avoid the table all together it's faster. This runs faster on my machine. You'll notice that My numbers are different than Jeffs too. That's simply because I mirror the numbers on the end then go x points out from the center (rather than last x points). Also this has weighting of missing values so if you have any missing values it's a non issue. At least I think so. If you don't need a column at the end it's even faster too. And the since it's just basically a concatted index matrix, it's pretty quick.
Names Default to here(1);
dt = open("$SAMPLE_DATA\Big Class.jmp");
st1 = HPtime();
mat = :height << Get Values;
//number of rows you want to average
x= 5;
//+- gap
z = (x-1)/2;
//get the rows
rows = 1::nrows(mat);
//mirror the rows on the front and back
mirrored = ((z+1)::2)||rows||((ncol(rows)-1)::(ncol(rows)-z));
big_mat = [];
for(i=0, i<=x-1, i++,
//this is cutting up the longer mirrored vector into x vectors of the same length as the original
big_mat ||= mat[mirrored[rows+i]];
);
//now we can just take a VSum of the transpose /x to get our average
Squasher = !ismissing(big_mat); //everywhere there's a non-missing, make 1
Squasher = VSum(Squasher`); //count real numbers, this is to not weight non-missings
A = Vsum(big_mat`)/x;
New Column("Moving Average", Set Values(A)); //If you don't need this column
//and you're just doing matrix operations this is actually about half the total time
en1 = HPTime()-st1;
// Data Table method
st2 = HPTime();
dt<< New Column("moving sum(x)", formula(If(Row()<=:Moving Avg Window,
If( Row() == 1,
:height,
Lag( :Name( "moving sum(x)" ), 1 ) + :height
),
(Lag( :Name( "moving sum(x)" ), 1 ) + :height) -
Lag( :height, :Moving Avg Window )
)));
dt<< New Column("Moving Avg", Formula(
If(Row()>=:Moving Avg Window,
:Name( "moving sum(x)" ) / :Moving Avg Window,
.
)));
en2 = HPTime()-st2;
show(en1, en2);Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us