- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: DoE for Optimization of Chromatography Conditions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
DoE for Optimization of Chromatography Conditions
Hi All,
I'm hoping for some guidance/support in setting up a DoE to optimize a few parameters in an HPLC separation.
In total I have 4 factors, all are continuous (three are chemical compositions of the mobile phase, 1 is column temperature).
I am anticipating cross effects between some of the conditions that will impact the responses in my study.
What is the best approach to DoE here? Should I be running a definitive screening design or a custom design with higher-order interactions (4th)? When I set up the custom design I'm not seeing any center point conditions for any of the factors at all. Is this a problem? Will I still see quadratic effects? When I set up the definitive screening design I do see some 2-way cross effects indicated...but I'm concerned that I'll be missing other potential interactions.
Any tips or advice would be greatly appreciated....thanks in advance!
Chris
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE for Optimization of Chromatography Conditions
When optimization is the goal, Definitive Screening designs aren't the first design I'd pick. Reason being, they are screening designs first and foremost with some unique properties, but screening designs nonetheless. So where are you in your depth, breadth, and maturity of the process/problem at hand? Are you screening factors or are past that? In other words, you know the key factors, levels of those factors which will surround the factor space optimal position, have a good handle on noise variables (controlled and uncontrolled), and a good idea of the model you'd like to fit?
If you are truly screening factors, a DSD isn't a bad way to go. It will give some insight for future, sequential experimentation. But if you are past screening, then a model driven optimal design approach is probably the way to go. If you want quadratic effects in the model, specify them and the coordinate exchange algorithm will provide the proper levels for the factors to estimate those effects as well as any interaction effects you seek.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE for Optimization of Chromatography Conditions
Echoing @P_Bartell 's comment: If you're thinking there are higher order factors at play, then DSD might not be the best place to start. The Custom Designer might be a better option for the experimental design, as it is usually better when you start with a model that you've defined for your exact circumstances.
Also, do you have JMP or JMP Pro? In JMP Pro, the Functional Data Explorer platform can analyze the entire output stream of each HPLC column as a single response, allowing you to specify the entire desired curve/spectra that you're looking for. The sample file NMR DOE.jmp that comes with JMP has an example of this.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE for Optimization of Chromatography Conditions
Thanks for the input. I don't have JMP Pro...but this is a great motivation to get it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE for Optimization of Chromatography Conditions
Hi @ClusterFerret68,
Just to be sure, the three chemical compositions of the mobile phase are three independent continuous factors, not mixture (dependent) factors that sum up to a constant value ?
If all the factors are continuous and your goal is optimization, traditional "textbooks" DoEs commonly met for chromatography process optimization are Central Composite Design (CCD) and Box-Benhken. See more infos about it in one of my previous response : Solved: Re: Optimization task with 2 continuous and 1 discrete (2 levels) factors - JMP User Communi...
You can also use the Custom Design platform, specify your factors, and create a Response Surface Model by clicking on "RSM" in the "Model" panel : all 2-factors interactions and quadratic effects will automatically be added in the model, the design will be I-optimal (to minimize average prediction variance over the experimental space) for a recommended default number of runs equal to 21.
Here is the script to generate such design :
DOE(
Custom Design,
{Add Response( Maximize, "Y", ., ., . ),
Add Factor( Continuous, -1, 1, "X1", 0 ),
Add Factor( Continuous, -1, 1, "X2", 0 ),
Add Factor( Continuous, -1, 1, "X3", 0 ),
Add Factor( Continuous, -1, 1, "X4", 0 ), Set Random Seed( 1822801991 ),
Number of Starts( 8853 ), Add Term( {1, 0} ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {3, 1} ), Add Term( {4, 1} ), Add Term( {1, 2} ),
Add Term( {1, 1}, {2, 1} ), Add Term( {2, 2} ), Add Term( {1, 1}, {3, 1} ),
Add Term( {2, 1}, {3, 1} ), Add Term( {3, 2} ), Add Term( {1, 1}, {4, 1} ),
Add Term( {2, 1}, {4, 1} ), Add Term( {3, 1}, {4, 1} ), Add Term( {4, 2} ),
Set Sample Size( 21 ), Optimality Criterion( "Make I-Optimal Design" ),
Simulate Responses( 0 ), Save X Matrix( 0 ), Make Design}
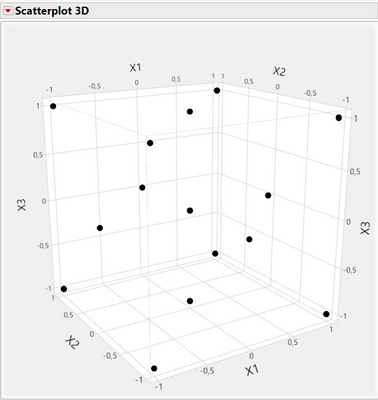
)And in 3D the repartition of points look similar to a Central Composite Design (which would need 26 runs for 4 continuous factors) when you specify axial value of 1 (axial points "on face") :
I wouldn't add more terms or higher power in the model (except if domain expertise or previous experience give you strong hints about the usefulness of these terms in the model), and first check the results from this modeling on the measurements to see if the model is sufficient/reliable or if it needs an augmentation (and possibly include higher order terms).
I agree with previous answers about DSDs that this design is more adapted to a screening phase with large number of factors, not an optimization phase with a low number of factors.
DSDs are not recommended for less than 5+ factors, as you will need 13 runs (17 if you follow the default settings and recommendations from JMP with the 4 extra runs added) for up to 6 factors. So with a low number of factors, Custom Design would be less expensive in terms of experimental budget, with a greater flexibility to handle constraints and various factors types.
Numbers of runs needed for DSD with m factors are :
- 2m+1 for even numbers of factors
- 2m+3 for odd numbers of factors.
More infos on DSDs can be found in the Learning Center : Definitive Screening Design - JMP User Community
Similar presentation topics from the Community :
I hope this first answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE for Optimization of Chromatography Conditions
My preference is the Custom DOE platform cfr. presentation Optimization of UHPLC measurement system. You can try DSD and Custom and compare both in doe diagnostics menu . My guess is that for custom doe you will get a higher power for interaction effects which is quite important. There may be - because of little negigible correlation - somewhat lower but still acceptable high power for main & quadratic effects.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE for Optimization of Chromatography Conditions
Thanks Victor! I'll start down this path. Appreciate your input greatly!
Chris
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us