- JMP User Community
- :
- Discussions
- :
- DoE Continuous Mixture Factors with Continuous and categorical response
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
DoE Continuous Mixture Factors with Continuous and categorical response
What should be the modeling for this kind of DoE? Any tips or steps are much appreciated.
Thank you guys. Much love
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
Hi @Alainmd02 ,
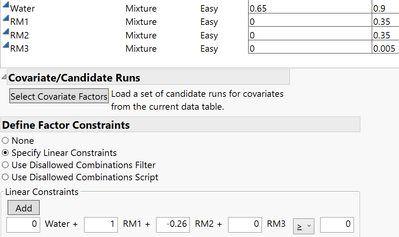
You need to set this up with a linear constraint to define that the ratio of RM1:RM2 >= 0.26.
I find the best way to get the equation for the constraint is to define 2 points that obey the constraint (e.g. 0.1, 0.385 and 1,3.85) and fit a line using Fit Y by X in JMP.
This gives you the equation, RM1 = 0 + 0.2597403*RM2, and you just need to rearrange into a form that fits the constraints interface.
Here is the script for the Custom Design.
DOE(
Custom Design,
{Add Response( Maximize, "Y", ., ., . ),
Add Factor( Mixture, 0.65, 0.9, "Water", 0 ),
Add Factor( Mixture, 0, 0.35, "RM1", 0 ),
Add Factor( Mixture, 0, 0.35, "RM2", 0 ),
Add Factor( Mixture, 0, 0.005, "RM3", 0 ), Set Random Seed( 2095116882 ),
Number of Starts( 29816 ), Add Constraint( [0 -1 0.26 0 0] ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {3, 1} ), Add Term( {4, 1} ),
Add Alias Term( {1, 1}, {2, 1} ), Add Alias Term( {1, 1}, {3, 1} ),
Add Alias Term( {1, 1}, {4, 1} ), Add Alias Term( {2, 1}, {3, 1} ),
Add Alias Term( {2, 1}, {4, 1} ), Add Alias Term( {3, 1}, {4, 1} ),
Set Sample Size( 10 ), Simulate Responses( 0 ), Save X Matrix( 0 ),
Set Run Order( Randomize ), Make Table}
);
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
I have the following thoughts:
1. Did you look at the correlation of the response variables?
2. I don't understand why you would have a nominal response for mixture design? The analysis should give you contour plots for each response variable which, of course, is non-sensical for a nominal response. What is passing or failing? Can that be converted into a continuous response?
3. Phil already commented on your constant factor ratio.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
Hi @stats
1. What do you mean by looking at the correlation of the response variables?
2. The binary nominal response. is Clear solution and Hazy solution . I want my product to be a clear solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
1. Whenever you have multiple response variables, it is prudent to assess the relationship between the response variables. Particularly when some of the response variables have potential measurement system issues (e.g., lack discrimination, resolution, or precision, are unstable). Plotting the response variables on scatter plots, checking for outliers with Mahalanobis are easy ways to look for those associations (Analyze>Multivariate Methods>Multivariate).
2. I believe, perhaps with a little work, this response could be made more continuous (e.g., measure opacity, shine a light source through the solution, why is the clarity changing? Is it due to solids? Measure solids in the solutions). If nothing else, you aught to be able to rank order the clarity of the solution and use an ordinal response. It all relates to efficiency. To see changes in nominal response variables you typically need larger sample sizes. As the response becomes more continuous you can get the information you need with less samples. In addition, many nominal response variables are aggregate. They change as a result of multiple failure mechanisms. This creates a real challenge when trying to understand causal structure.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
@statman and @Alainmd02 .
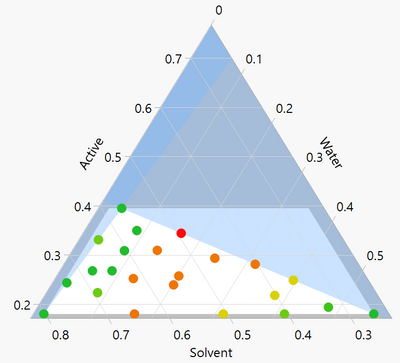
Regarding 2.: I did something like this in a project when I was working in the chemicals industry. We had the same aim, which was to understand what parts of the formulation space gave us clear, homogeneous solutions. We rated clarity on a scale of 1-5. And we also heated up the samples to 70C and rated them as they cooled to 60, 50, 40, 30 and 20. I struggled to build useful statistical models of the data. The visuals of this data were very useful though. Here is a plot of the (anonymised) data for 20C. You can clearly see the good, green regions. That was all we needed to know for our objectives.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
This is interesting. Its almost the same as my experiments.
Much appreciated Phil.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Continuous Mixture Factors with Continuous and categorical response
I think this solved our problem. It is easier if we have continuous responses. That's why we found a way to quantify the clarity levels of our solutions.
Kudos to you @statman
Much Appreciated.
- « Previous
-
- 1
- 2
- Next »
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us