- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- DoE Augmentation three options not available
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
DoE Augmentation three options not available
Hi all,
I have completed a screening experiment looking at the main effects. The model becomes highly significant if I add interaction factors during analysis.
Now I want to augment the design and want to add the center point and RSM as well. Under the augmentation choices box, only options available are Replicate, Space Filling and Augment whereas Add Centerpoints, Fold Over, and Add Axial are greyed. Any reason why this could be?
Many thanks.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Augmentation three options not available
Hi @Do_AuLu,
The results you obtained can be completely normal and dependent of the factors type you have.
- If you have only continuous factors, all augmentation options are available.
- If you have one (or several) 2-levels categorical factors (and the rest is only continuous factors), then "Add Axial" and "Space-Filling" are not possible (greyed out).
- If you have one (or several) 3-levels categorical factors (and the rest is only continuous factors), then "Fold Over", "Add Axial" and "Space-Filling" are not possible.
Depending on the original design and factors type, some augmentation choices may be restricted. You can find more information here : Augmentation Choices
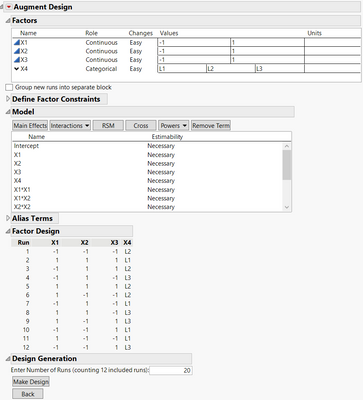
Even if the option "Add Centerpoints" is unavailable, you may be able to continue with your design augmentation by choosing "Augment", and from there in the "Model" tab click on "RSM" to augment your initial screening design in a Response Surface Design with 2-factors interactions and quadratic effects terms :
As you're using Custom Design, this is probably the most straightforward option, and the possibility to add centerpoints may not be very useful if you already assume a RSM model, as they don't improve the estimation of model effects (but can be interesting to consider if your experimental space is centered around your optimal settings, to evaluate robustness of this optimum). Centerpoints (when available) are great for detecting curvature, but since you augment your design to add quadratic terms in the model, you'll already be able to estimate these quadratic effects (if present). More info on centerpoints here : Center Points, Replicate Runs, and Testing (jmp.com)
As a general recommendation, I would also recommend to check the option "Group new runs into separate block" to add a blocking variable in your design. This precaution will add in your model a fixed block effect, which might help you detecting any mean response(s) shift between your first set of experiments and the next (augmented) set of experiments (a change in the intercept of the response(s)).
Depending on how you see the variation, you can also change the block effect from "fixed" to "random" to evaluate if you have a difference on the random error (variance) between your two sets of experiments.
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: DoE Augmentation three options not available
Hi @Do_AuLu,
The results you obtained can be completely normal and dependent of the factors type you have.
- If you have only continuous factors, all augmentation options are available.
- If you have one (or several) 2-levels categorical factors (and the rest is only continuous factors), then "Add Axial" and "Space-Filling" are not possible (greyed out).
- If you have one (or several) 3-levels categorical factors (and the rest is only continuous factors), then "Fold Over", "Add Axial" and "Space-Filling" are not possible.
Depending on the original design and factors type, some augmentation choices may be restricted. You can find more information here : Augmentation Choices
Even if the option "Add Centerpoints" is unavailable, you may be able to continue with your design augmentation by choosing "Augment", and from there in the "Model" tab click on "RSM" to augment your initial screening design in a Response Surface Design with 2-factors interactions and quadratic effects terms :
As you're using Custom Design, this is probably the most straightforward option, and the possibility to add centerpoints may not be very useful if you already assume a RSM model, as they don't improve the estimation of model effects (but can be interesting to consider if your experimental space is centered around your optimal settings, to evaluate robustness of this optimum). Centerpoints (when available) are great for detecting curvature, but since you augment your design to add quadratic terms in the model, you'll already be able to estimate these quadratic effects (if present). More info on centerpoints here : Center Points, Replicate Runs, and Testing (jmp.com)
As a general recommendation, I would also recommend to check the option "Group new runs into separate block" to add a blocking variable in your design. This precaution will add in your model a fixed block effect, which might help you detecting any mean response(s) shift between your first set of experiments and the next (augmented) set of experiments (a change in the intercept of the response(s)).
Depending on how you see the variation, you can also change the block effect from "fixed" to "random" to evaluate if you have a difference on the random error (variance) between your two sets of experiments.
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us