- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Distributions and Curves Intersection
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Distributions and Curves Intersection
Dear Community I have a need to be solved (I do not found similar question in blog).
I have 2 set of data.
I created the 2 distributions.
I "aks to JMP" to found the better curve fit for each single distribution.
Now I need to found the intersetion point (X= ...) between the 2 curves.
In attachement you can find the example of dataset and the visualization of what I need.
Thanks in advance for your feedback.
Best Regards.
Simone
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Here is a crude script that will get you the values. Not sure it will work for all comparisons...but it might. Try it out. The results display in the log.
Names Default To Here( 1 );
dt = Current Data Table();
// Change these values to the actual values of the 2 distributions
m1 = 203.315;
s1 = 203.33 - m1;
max1 = 203.37;
m2 = 203.345;
s2 = 203.355 - m2;
max2 = 203.4;
If( Normal Density( min(m1,m2), mu = m1, sigma = s1 ) > Normal Density( min(m1,m2), mu = m2, sigma = s2 ),
mh = m1;
sh = s1;
ml = m2;
sl = s2;
,
mh = m2;
sh = s2;
ml = m1;
sl = s1;
);
For( i = ml, i <= Min( max1, max2 ), i = i + ((Min( max1, max2 ) - ml) / 1000000),
r = i;
nd1 = Normal Density( r, mu = mh, sigma = sh );
nd2 = Normal Density( r, mu = ml, sigma = sl );
lastnd1 = nd1;
lastnd2 = nd2;
lasti = i;
If( nd2 > nd1,
x = Mean( i, lasti ); y = Mean( nd1, nd2, lastnd1, lastnd2 );
show(x,y) ;
Break();
);
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Once you have the formula columns saved (in this case for two Gaussians), you can get a long way by using the crosshair tool.
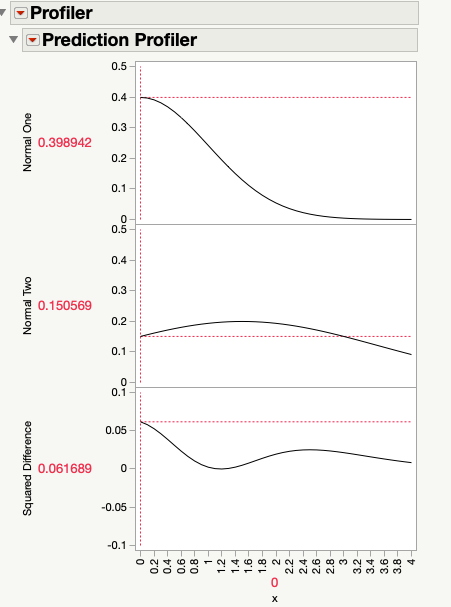
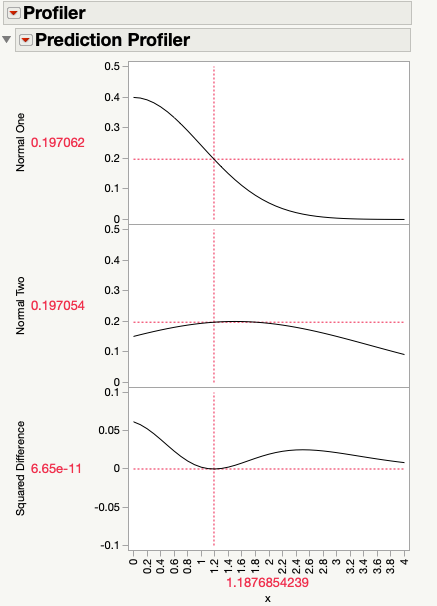
But if you want an 'exact' answer, you could define an auxiliary formula column and use 'Maximize Desirability' in the Profiler (see the attached table). But note that you still need to inspect the plots, and use the Response Limits column property to restrict the range of the optimization appropriately. In this example, I also used this property with the two original columns (with a weight of zero) just to allow all three columns to be profiled at the same time.
Before:
After:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
I believe that there is no direct way. That is to say, there is no platform with this capability. You could use the Minimize() function with the difference between the two probability density functions using their respective estimated distribution parameters in a script. The independent variable is the quantile.
Please provide data and examples in JMP files, not Excel files in the future.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Dear Mark,
thank you for the feedback.
I "hoped" there was some capability to do this in JMP...
Regarding you suggestion... I will try to follow it (even if I'm not an expert in the JMP Script).
Have you a good day.
Best Regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Once you have the formula columns saved (in this case for two Gaussians), you can get a long way by using the crosshair tool.
But if you want an 'exact' answer, you could define an auxiliary formula column and use 'Maximize Desirability' in the Profiler (see the attached table). But note that you still need to inspect the plots, and use the Response Limits column property to restrict the range of the optimization appropriately. In this example, I also used this property with the two original columns (with a weight of zero) just to allow all three columns to be profiled at the same time.
Before:
After:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Thanks Ian.
Appreciated your good feedback.
Best Regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Here is a crude script that will get you the values. Not sure it will work for all comparisons...but it might. Try it out. The results display in the log.
Names Default To Here( 1 );
dt = Current Data Table();
// Change these values to the actual values of the 2 distributions
m1 = 203.315;
s1 = 203.33 - m1;
max1 = 203.37;
m2 = 203.345;
s2 = 203.355 - m2;
max2 = 203.4;
If( Normal Density( min(m1,m2), mu = m1, sigma = s1 ) > Normal Density( min(m1,m2), mu = m2, sigma = s2 ),
mh = m1;
sh = s1;
ml = m2;
sl = s2;
,
mh = m2;
sh = s2;
ml = m1;
sl = s1;
);
For( i = ml, i <= Min( max1, max2 ), i = i + ((Min( max1, max2 ) - ml) / 1000000),
r = i;
nd1 = Normal Density( r, mu = mh, sigma = sh );
nd2 = Normal Density( r, mu = ml, sigma = sl );
lastnd1 = nd1;
lastnd2 = nd2;
lasti = i;
If( nd2 > nd1,
x = Mean( i, lasti ); y = Mean( nd1, nd2, lastnd1, lastnd2 );
show(x,y) ;
Break();
);
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Hello Jim,
thanks for the feedback.
I will apply it!
Best Regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Hey Jim, What are the M, S and max values?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Distributions and Curves Intersection
Mean, Sigma and Max
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us