- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Deviance goodness of fit test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Deviance goodness of fit test
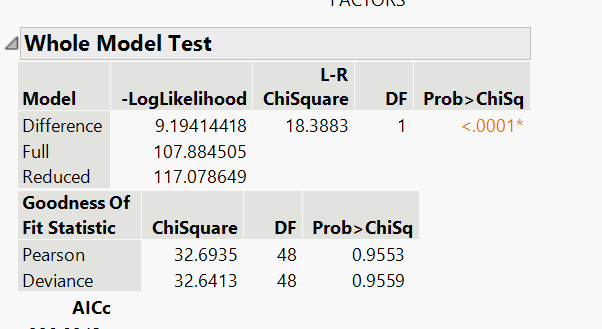
Hi can someone help me interpret both Pearson and Deviance goodness of fit test in the context of Poisson's regression? I am trying to determine if X= # of factors (aka medical items used on a patient can determine their length of stay in days (Y). My overall model is significant but my goodness of fit stats are not. See below, also i should note both my intercept and x parameter are significant
Thank you
#STATISTICS
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Deviance goodness of fit test
There are two tests for goodness of fit. These two hypothesis tests assume that the fit is good (null hypothesis). The alternative hypothesis (test) is that there is lack of fit. They both estimate a Chi square sample statistic. They are both based on the change in the negative log likelihood between the full model (fitted) and the saturated model. A significant test indicates lack of fit. The Pearson test is older.
The two methods of estimating Chi square yield very similar estimates. The choice of alpha (level of significance required) is up to you but your example does not appear to exhibit lack of fit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Deviance goodness of fit test
There are many ways to think about (i.e., hypothesize) tests. The common whole model test assumes (null hypothesis) that the model is not significant. Another way to say it is that all the parameters (except for the constant) are 0. The alternative hypothesis is that not all the parameters are 0. So you might think about the whole model test as a way to answer the question, "Are any of the terms in this model significant?" You can also ask this question of individual terms, of course.
The goodness of fit test is asking, "Is there evidence that I am missing terms in the model for residual effects in the response?" That is a concern for lack of fit. So the test assumes (null hypothesis) that the model is a good fit. The alternative hypothesis is that the model is not a good fit because it seems that there is variation in the response that is not entirely accounted for by the variance part of the model. The saturated model provides the estimate of the variance so that it can be compared to the variance of the fitted model. They won't be identical, but is the difference unusual (statistically significant)?
Perhaps we should talk about a good model versus a better model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Deviance goodness of fit test
There are two tests for goodness of fit. These two hypothesis tests assume that the fit is good (null hypothesis). The alternative hypothesis (test) is that there is lack of fit. They both estimate a Chi square sample statistic. They are both based on the change in the negative log likelihood between the full model (fitted) and the saturated model. A significant test indicates lack of fit. The Pearson test is older.
The two methods of estimating Chi square yield very similar estimates. The choice of alpha (level of significance required) is up to you but your example does not appear to exhibit lack of fit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Deviance goodness of fit test
Thank you! I just wanted to make sure in this case they were flipped from traditional hypothesis test and that you didn't want a significant p-value you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Deviance goodness of fit test
@Mark_Bailey can I ask you another question? Bare with me if I sound dumb, my stat's teacher is sending me for a loop....
So we have the whole model test and then the Goodness of fit test's. My teacher has implied to use the Whole Model Test to determine overall significance for the model. He also said when doing this the
Ho: model is not significant
Ha: model IS significant
Which here would make sense with what I have set up for the Whole model test, and my p-value is less than my alpha (.05).
Are you then saying that then I use a different "set of hypothesis" set up like this for Goodness of fit:
Ho: the model is statistically significant for determining my y-variable
Ha: the model is NOT statistically significant for determining my y-variable.
Because in my mind and the context of my data this is the only way to have my whole test indicate model be significance and also then have my goodness of fit statistics indicate a good model fit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Deviance goodness of fit test
There are many ways to think about (i.e., hypothesize) tests. The common whole model test assumes (null hypothesis) that the model is not significant. Another way to say it is that all the parameters (except for the constant) are 0. The alternative hypothesis is that not all the parameters are 0. So you might think about the whole model test as a way to answer the question, "Are any of the terms in this model significant?" You can also ask this question of individual terms, of course.
The goodness of fit test is asking, "Is there evidence that I am missing terms in the model for residual effects in the response?" That is a concern for lack of fit. So the test assumes (null hypothesis) that the model is a good fit. The alternative hypothesis is that the model is not a good fit because it seems that there is variation in the response that is not entirely accounted for by the variance part of the model. The saturated model provides the estimate of the variance so that it can be compared to the variance of the fitted model. They won't be identical, but is the difference unusual (statistically significant)?
Perhaps we should talk about a good model versus a better model.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us