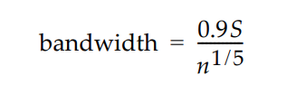- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Default Kernel Std in Smooth Curve fit (Distribution Platform)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Default Kernel Std in Smooth Curve fit (Distribution Platform)
Without luck, I have looked for any details on how JMP sets the default Kernel Std in the manuals. I have also experimented with ratios between StdDev (or SE) and default Kernel Std for datasets of different size in order to find any consistent pattern.
Does anyone know how JMP chooses the default Kernel Std, i.e. the one showing up initially before the user touches the slider?
And, second, is it possible to set the Kernel Std by JSL-script?
Message was edited by: MS
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Default Kernel Std in Smooth Curve fit (Distribution Platform)
Since this post was written in 2009, JMPs documentation and methods have been updated a bit so I wanted to take a moment to provide a more current answer to the original question in light of that. While I can't comment on method/s to set the Kernel Std by JSL, the default estimation of the "Kernel Std" (in the Legacy Fitter for Smooth Curve prior to JMP 15), otherwise known as the Kernel "Bandwidth" (in the Modern Fitters available in JMP 15 and up), is:
where S is the sample standard deviation and n is the sample size. This is per the JMP 17.0.0 Documentation Library, https://www.jmp.com/content/dam/jmp/documents/en/support/jmp17/jmp-documentation-library.pdf, see Chapter 9, Quality and Process Methods p. 262 of that book (p. 4778 of 7206 of the compiled PDF). Note that the same formula and reference can be found in the online version of JMP's support documentation, here: https://www.jmp.com/support/help/en/17.0/#page/jmp/individual-detail-reports.shtml#
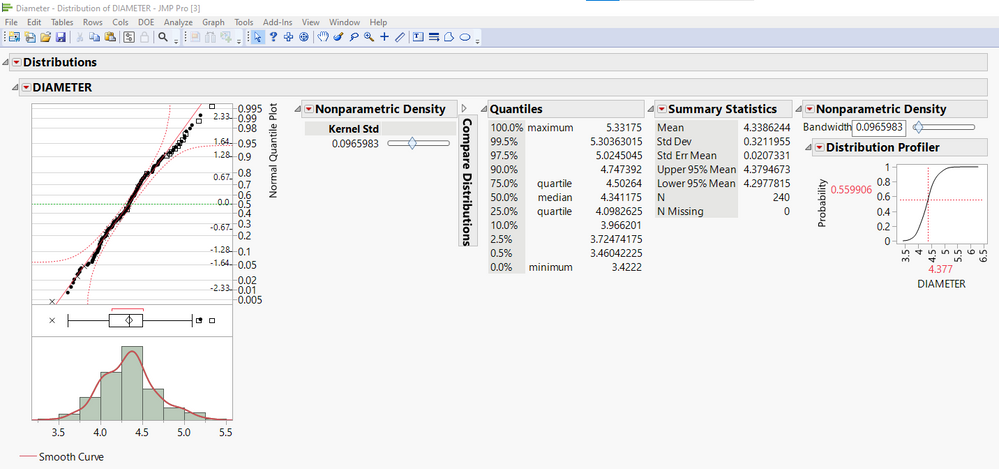
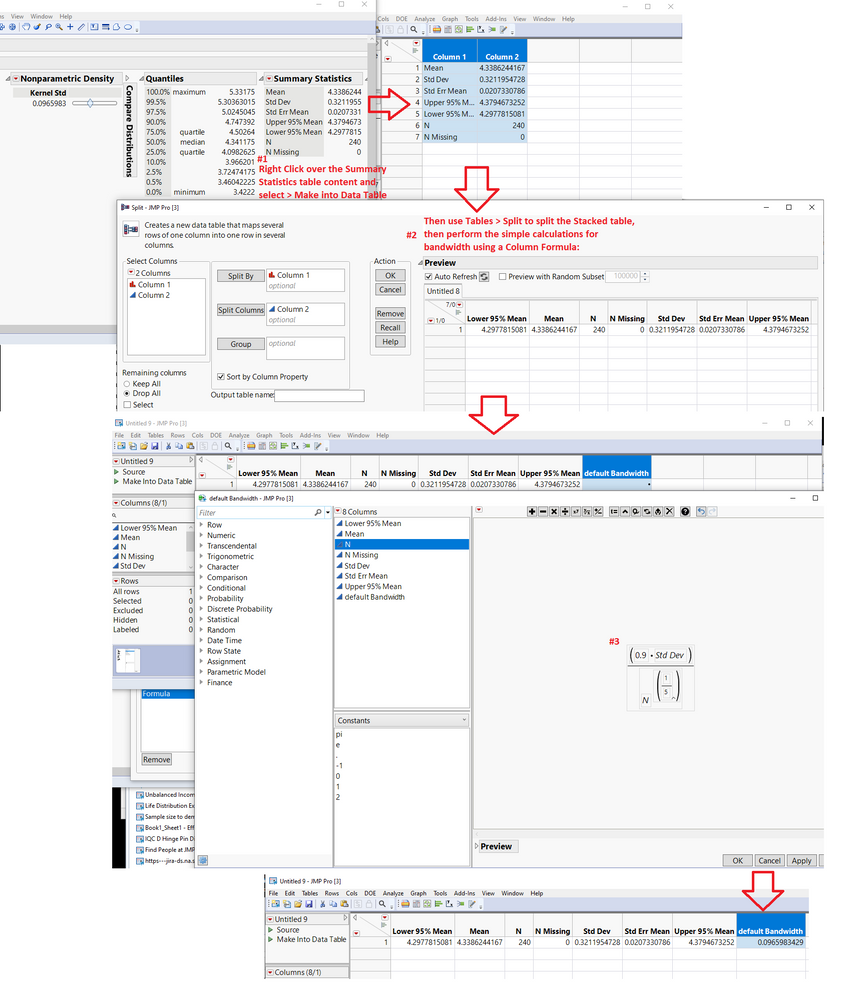
You can test this out on the Diameter.jmp sample dataset, where in this case I am showing the Distribution summary statics with both the legacy and current version of the Smooth Curve Fitters invoked, where the Kernel Std = Bandwidth = 0.0965983 by default:
Bandwidth = (0.9*(0.32119547))/(240)^(1/5) = 0.0965983
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Default Kernel Std in Smooth Curve fit (Distribution Platform)
The Distribution platform in JMP v9 will feature a new distribution you can fit, called Normal Mixtures. If a distribution is multi-modal, it fits a normal distribution (with a separate mean and variance) to each group. The pdf ends up being a weighted sum of the component pdfs. Well, I tell you this because the Smooth Curve is just a special case of the Normal Mixture. If you fit enough groups, the Normal Mixture fit is essentially identical to the Smooth Curve fit. But, the Normal Mixture fit has a big advantage in that it is much easier to understand and explain.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Default Kernel Std in Smooth Curve fit (Distribution Platform)
Why i am asking is because I try to figure out a if I can use quantiles for the smooth curve fit as a robust way to routinely identify outliers in interlaboratory tests, in cases where the distribution is clearly asymmetric or multimodal. The quantiles I can set and retrieve via JSL but I am not sure if I can trust the default Kernel Std to be adequate for each round of tests which may have different number of participants or distribution shape.
It would be neat to be able to set the Kernel Std to e.g. 3/4 of the standard deviation (or whatever) by JSL. But maybe the JMP definition and default choice, although too complicated to document, is good enough to allow comparison of the kernel density quantiles among different sets of data.
In some textbooks or other statistical software's documentation it is referred to the kernel density "bandwidth". Is that comparable to JMPs Kernel Std?
(Btw I look forward to JMP v9 and as a Macintosh user I would very much welcome the return of, at least some rudimentary, Applescript support)
Message was edited by: MS
Message was edited by: MS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Default Kernel Std in Smooth Curve fit (Distribution Platform)
Probably a bit late, but I found the post looking for setting the kernel value. Here is a solution for creating a reproducible smooth fit with adjusted bandwidth in case somebody looks for it again. I hope though that the Jmp team improves on that...
dt = Open( "$SAMPLE_DATA/Big Class.jmp" );
dst=Distribution(
Automatic Recalc( 1 ),
Continuous Distribution(
Column( :height ),
Vertical( 0 ),
Fit Distribution( Smooth Curve ),
Confidence Interval( 0.95 )
),
Histograms Only
);
dstr=dst<<Report;
dstr[Sliderbox(1)]<<set value(0.7);
npd=dstr[OutlineBox(3)]<<Get Scriptable Object;
npd<<Quantiles( 0.00135, 0.99865 );- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Default Kernel Std in Smooth Curve fit (Distribution Platform)
If data is just simply asymmetric, then many of the available distributions will fit it. Particularly the Johnson distributions and Glog. They can handle heavy skewness. If it's not too skewed, then perhaps one of the common ones will work too, like Weibull or LogNornal. For different shapes of skewness, the fitted parameters will be different of course.
If data is multimodal, then the only option now is the smooth curve fit. If the shape of each data set is relatively the same, then the estimated kernel std will be roughly similar. If the shapes are very different, then the kernel std is different. Don't try to compare the kernel std's, but it is ok to make a rough comparison of the quantiles. I haven't formally investigated the performance of the smooth curve fit across different samples that are supposed to be similar or different, so I am guessing at these things. And, of course, quantiles can vary depending on overfitting or underfitting of the smooth curve.
If you want to estimate quantiles without worrying about a fitted distribution, there is an empirical quantile function in the formula editor, under the Statistical group. Table > Summary can also spit out quantiles
If you want to investigate for outliers, sometimes the best way to identify them is with the eye. Like on a histogram or the outlier box plot. But, I'm sure there is perhaps an automated/quantitative way to do it. What is an outlier to one fitted distribution, may not be to another fitted distribution though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Default Kernel Std in Smooth Curve fit (Distribution Platform)
Since this post was written in 2009, JMPs documentation and methods have been updated a bit so I wanted to take a moment to provide a more current answer to the original question in light of that. While I can't comment on method/s to set the Kernel Std by JSL, the default estimation of the "Kernel Std" (in the Legacy Fitter for Smooth Curve prior to JMP 15), otherwise known as the Kernel "Bandwidth" (in the Modern Fitters available in JMP 15 and up), is:
where S is the sample standard deviation and n is the sample size. This is per the JMP 17.0.0 Documentation Library, https://www.jmp.com/content/dam/jmp/documents/en/support/jmp17/jmp-documentation-library.pdf, see Chapter 9, Quality and Process Methods p. 262 of that book (p. 4778 of 7206 of the compiled PDF). Note that the same formula and reference can be found in the online version of JMP's support documentation, here: https://www.jmp.com/support/help/en/17.0/#page/jmp/individual-detail-reports.shtml#
You can test this out on the Diameter.jmp sample dataset, where in this case I am showing the Distribution summary statics with both the legacy and current version of the Smooth Curve Fitters invoked, where the Kernel Std = Bandwidth = 0.0965983 by default:
Bandwidth = (0.9*(0.32119547))/(240)^(1/5) = 0.0965983
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us