DOE Vocabulary Clarification

[#1]

I am tired of just ignoring a nagging concern I've had about DOE vocabulary, as I'm wondering if I don't fully understand a concept. I find that ALIASING, CORRELATION and CONFOUNDING show up in many discussions, and sometimes seem to be used interchangeably.  For example, the DOE platform in JMP provides wonderful color correlation maps that I use extensively when evaluating a potential design, but also has an alias matrix. In many places the term "confounding" of a main effect with a two-factor interaction is used.

I understand the concept and importance of confounding, which is the term I most often use, so I'm not asking for a discussion of what that is in the context of, for example, RES III versus RES V designs. My question is about the precise definition of each of these three terms. As I said, they sometimes give the appearance of being different names for the same thing, but I'm not convinced that is the case.

I'd appreciate clarification on this point. If they ARE all the same thing, why do we have different terms in use? If they aren't, I really need to understand the precise meaning and usage for each term.

Thanks in advance.

[#2]

To me, confounding, aliasing, and correlation are NOT the same.  When setting up a DOE, the column signs can be multiplied, and the resulting sign being another column which can be used for another factor.  Thus that factor is "aliased" by the new column.  For example, you might decide that a three-way interaction between X1, X2, and X3 is very unlikely, so you set a column by multiplying the signs of those three factors and use the column for a 4th factor.

Confounding is when the signs of some columns happen to be the same.  For example, you might find that when setting up the trial matrix, the interaction column X1X2 might have the same signs as X2X3X4.  In other words, the effect of X1X2 cannot be separated from the effect of X2X3X4 - they are confounded.

Correlation is different in that two (or more) factors tend to move together or in opposing paths together.  Remember that correlation does not mean "cause and effect".  There may be other factors that cause the two (or more) correlated factors to move the way they do.

[#3]

My simplistic way of thinking of these concepts is as follows:

A two step workflow is involved:

Step 1: Evaluate a design for the presence of confounding and aliasing among any effects which are intended to be estimated. I consider this action and the phrases to be synonymous. Kind of like asking, "Are you pregnant/expecting a baby?"...either you are or are not. That is, any one design either has confounding/aliasing present for at least one effect or it does not. Then, if the answer is no. Stop...there is zero correlation between any two effects. If the answer is "Yes, there is confounding or correlation within this design." Then proceed to step 2.

Step 2: The next logical question is which effects are confounded or aliased with which? And what is the degree of bias associated with these effects? That's where correlation comes in. Which is why many find the JMP Color Map on Correlations a great visual aid to evaluate a design. Correlation is a measure of the bias associated with parameter estimates.

There is an explanation of these issues in the JMP version 12 native Help with the software if you just invoke from the JMP main menu:

Help -> Search the Help, enter Design Evaluation Window in the Search field, and select the topic Design Evaluation Window.

[#4]

The Color Map on Correlations gives you an idea as to the relationship between the effects in your model and those that are not in your model, but may have an effect on the response (alias terms). In addition to the DOE guide mentioned above, you can take a look at this blog: Correlation cell plot for design comparison in JMP

Confounding of two effects means that there's no way to distinguish between the two effects. Follow-up runs would be needed to differentiate these effects, and/or assumptions will need to be made about which effects are negligible. You will see this also called aliasing, but I like to think of this as full aliasing. You can have partial aliasing, where the effects are neither orthogonal nor fully aliased/confounded (think of entries in the Color Map on Correlations that are not 0 or 1).

The Alias Matrix reflects the degree to which effects not in the model can bias the effect estimates. If you have partial aliasing for effects in the model, your standard errors for effect estimates are larger. More information in this blog: http://blogs.sas.com/content/jmp/2014/06/05/what-is-an-alias-matrix/

Hope that helps clarify things.

Cheers,

Ryan

[#5]

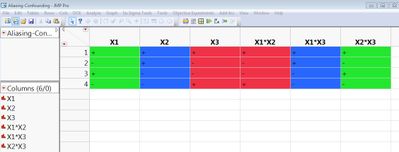
Below is a picture of what Aliasing/Confounding looks like for 2 level continuous factors.  Multiply the signs of the main effects as shown to get the corresponding sign for that interaction.  * = for Row 1 X1*X2 as an example.  As you can see in the picture each main effect is completely confounded with one of the interaction terms which illustrates what has been stated above. So, you could not reliably use the interaction terms in your model knowing there is no distinction between the main effect and it's corresponding (color) interaction term.

[#6]

I probably didn't state my question well. I understand the color correlation maps, but find that in many cases the three terms I mentioned are used almost as if they are different names for the same thing.

Specifically, are these three statements all saying the same thing about some design I might have created?

1) there is a correlation between X1 and X3

2) there is confounding between X1 and X3

3) X1 and X3 are aliased

Sometimes, when reading a post or some documentation, I've seen these terms interchanged even in the same paragraph.

[#7]

If I may repeat myself:  Confounding, aliasing, and correlation are NOT the same.  When setting up a DOE, the column signs can be multiplied, and the resulting sign being another column which can be used for another factor.  Thus that factor is "aliased" by the new column.  For example, you might decide that a three-way interaction between X1, X2, and X3 is very unlikely, so you set a column by multiplying the signs of those three factors and use the column for a 4th factor.

Confounding is when the signs of some columns happen to be the same.  For example, you might find that when setting up the trial matrix, the interaction column X1X2 might have the same signs as X2X3X4.  In other words, the effect of X1X2 cannot be separated from the effect of X2X3X4 - they are confounded.

Correlation is different in that two (or more) factors tend to move together or in opposing paths together.  Remember that correlation does not mean "cause and effect".  There may be other factors that cause the two (or more) correlated factors to move the way they do.

[#8 · Accepted solution]

If the design is orthogonal, your effect estimates are uncorrelated with each other. When the design is not orthogonal, you may have some partial aliasing, in which case some of the effect estimates are correlated: those estimates change depending on if the other effect is in the model or not, and you may see larger standard errors on your effects if both are in the model. This doesn’t mean the factors X1 and X3 are correlated (unless you have some underlying constraints), but that the way the design has been chosen, their effect estimates are correlated. Most DOE books mention correlation when discussing effect estimates, but searching through the index you'll be more likely to see aliasing and confounding.

You still have 2 different cases, one in which there is partial aliasing:

1. There is a correlation between the main effect estimates of X1 and X3.
2. The main effect estimates of X1 and X3 are partially aliased.

And one for full aliasing:

1. The main effect estimates of X1 and X3 are fully correlated.
2. The main effect estimates of X1 and X3 are confounded.
3. The main effect estimates of X1 and X3 are fully aliased.

Some authors have their own preference for their terminology, and depending on the context don't make the distinction between partial and full aliasing. For example, in the classical screening designs, you're only dealing with orthogonal or fully aliased/confounded, so it's not uncommon to see the "fully" dropped in such a case. The documentation team has been working hard to remain consistent in the last few (and upcoming) versions of the DOE documentation.