- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Custom DoE screening design
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Custom DoE screening design
I have two very basic questions about custom DoE screening design.
1. If I only wanted to know which main effects are significant to my responses and use the custom main effect screening design with the default run numbers given by JMP, how can I be sure whether it is the main effect or other confounding two-way interaction that is really significant? If the model analysis shows factor A is significant but A is partially correlated with B*C, what factor(s) should be included in the optimization design later? I suppose only the main effects that are significant such as factor A should be further investigated for the optimization design following the main effect screening design but will B and C be missing if B*C partially correlated with factor A but B and C are not significant main effects from the screening DoE?
2. when I include some uncontrolled factors in the model, JMP does not show the color map for correlation any more. How can I evaluate the design with uncontrolled factors?
Thanks
LL
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
@JMP38401 , Here are my thoughts:
1. There are three principles we rely on for fractional factorials and screen designs:
Scarcity: There are relatively few significant effects (analogous to the Pareto Principle)
Hierarchy: 1st order > 2nd order >> 3rd order, etc.
Heredity: In order for an interaction to be significant at least one parent must be significant
Regarding your question, my advice is to predict the rank order model effects (at least through 2nd order). Your predictions as to which effects you believe would be reasonable and likely will impact design resolution selection. If all of your 1st order effects rank above 2nd order effects, then lower resolution seems reasonable to begin the iterative process of investigation. In fact, this is the hierarchy principle. Expand the number of factors (1st order effects) by confounding higher order effects.
2. If you suspect interaction effects (≥2nd order), then you might want to bump resolution to IV+.
3. I know I don't represent the bulk of the thinking on optimal designs. I am not a huge fan of "partial confounding" to create a more efficient design as if there are instances that do not make sense in the data analysis, the next iteration can be a difficult choice (e.g., fold over designs don't work).
4. I don't completely understand your second question. If you have covariates in the data table, you can certainly see the correlation between the covariates and the design factors. Multivariate Methods>Multivariate will provide scatterplots and selecting the options (red triangle) you can get color maps. Of course if you have many, you can get VIFs by right-clicking in the parameter estimates out put table and adding >Columns>VIFs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
All of the design evaluation information is a function of the design matrix, but the columns for the uncontrolled factors are empty.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
There is no absolute answer. It depends. The impact of correlation is variance inflation, which is bad. Perfect correlation (confounding) inflates the variance to infinity. But otherwise it depends on the variance that your start with. Small variance might tolerate a large correlation while a large variance will tolerate very little inflation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
"If I only wanted to know which main effects are significant to my responses and use the custom main effect screening design with the default run numbers given by JMP, how can I be sure whether it is the main effect or other confounding two-way interaction that is really significant?"
Enter the main effects in the term list under Model. Make sure that all the two-way interactions are in the term list under Alias. Click the red triangle at the top and select Optimality Criterion > Make Alias Optimal Design.
"If the model analysis shows factor A is significant but A is partially correlated with B*C, what factor(s) should be included in the optimization design later? I suppose only the main effects that are significant such as factor A should be further investigated for the optimization design following the main effect screening design but will B and C be missing if B*C partially correlated with factor A but B and C are not significant main effects from the screening DoE?"
If you suspect higher-order terms are potentially active, then there are two ways that I recommend. First, add all the potential terms in the Model list. Select these terms and click on Necessary in the Estimability column, then select If Possible. This change will produce two results. The first result is that the minimum number of runs will decrease because it is determined by the number of parameters that must be estimated. (You need to guess the number of actually active terms and add runs to the minimum for them.) The other way is to use a screening design like Definitive Screening Design. This way will work as long as it is a true screening situation in which the key screening principles hold. How many factors to you have? How many are likely to be active?
I do not know the answer to your second questions, off the top of my head. Perhaps someone else has that knowledge.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
Thank you for the quick reply!
"Enter the main effects in the term list under Model. Make sure that all the two-way interactions are in the term list under Alias. Click the red triangle at the top and select Optimality Criterion > Make Alias Optimal Design."
I tried this and did not see any changes in Alias Matrix under Design Evaluation of the models. Did I miss anything or how do I know the model is optimized for Alias? Sorry if I misunderstood how the "Make Alias Optimal Design" works by assuming I will see a lower correlation effect under Alias Matrix or the color map of correlation.
"(You need to guess the number of actually active terms and add runs to the minimum for them.)"
I have 7 continuous factors with 3 of them HTC. I also have 3 uncontrolled factors that I will record their values during my DoE runs so totally 10 factors. When I created the screening design using Custom DoE platform, I have 11 Minimum Number of Runs (10 factors plus the intercept) and 18 runs as Default. There are 45 two-way interactions under Alias Terms. If I suspect 10 out of those 45 two-way interactions could be active terms, your suggestion is to add those 10 two-way interaction to the Model, change their Estimability to If Possible, and add 10 runs to the minimum 11 runs to make it 21 runs total or add the 10 runs to the default 18 runs to make it 28 runs total? Since I have HTC factors in the model, the definitive screening design does not seem to work.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
The Custom Design is very flexible. It is possible to define a main effects model and the two-interaction alias matrix and still get correlations. For example, the number of runs might prevent an orthogonal design to be made. Think of 3 factors in 7 runs.
Can you post a picture of the custom design elements (factors, model, alias matrix, design, and correlation map)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
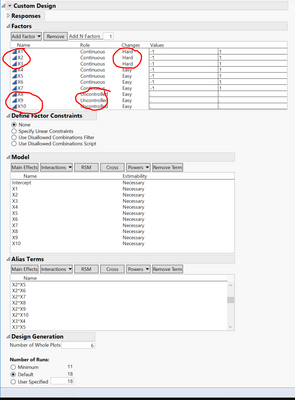
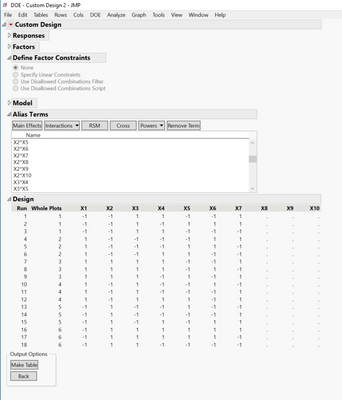
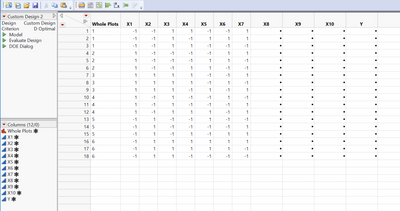
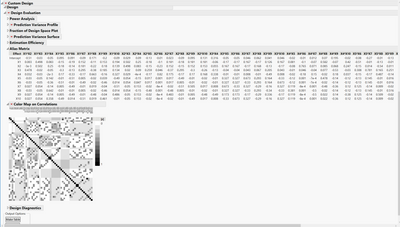
Above is the design with 10 factors (7 continuous factors with 3 of them HTC. 3 more uncontrolled factors.
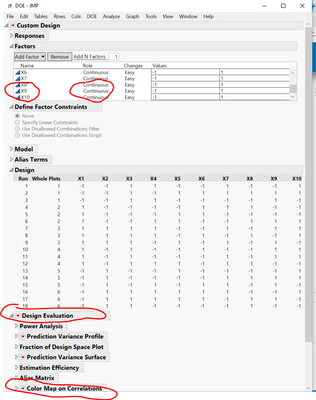
After I made the design, I don't see the Design Evaluation platform as I normally see when there is no Uncontrolled factors.
I had to click Make Table and then click DoE Dialog in order to see the Design Evaluation. However, when I checked the factors, X8, X9, and X10 became "Continuous" instead of the original "Uncontrolled". Not sure why and how that impacts the Design Evaluation. The last picture below shows the color map of correlation obtained this way.
My main question is whether this design is a good design to tell which main effect(s) out of those 10 factors are significant without worrying about their confounding with each other and other two-way interactions. My plan is to use those significant Main Effects out of this screening DoE for my next optimization DoE using RSM. Thank you very much!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
Just to add one thing, the correlation between X1 (HTC) and X2 (HTC) in the color map is 0.033, which sounds too big to me. Is there a suggested value for maximum correlation in order not to worry about the Aliasing? Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
It is a matter of signal to noise. A very large signal (non-zero parameter estimate) will be estimated well even if there is correlation. The correlation does not bias the estimate or the model. It inflates the standard error of the estimate. I consider 0.033 to be very small.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
Sorry for giving a wrong number, the correlation value is 0.33 instead of 0.033. I would think 0.33 will be too big but not sure how small is good enough. Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
There is no absolute answer. It depends. The impact of correlation is variance inflation, which is bad. Perfect correlation (confounding) inflates the variance to infinity. But otherwise it depends on the variance that your start with. Small variance might tolerate a large correlation while a large variance will tolerate very little inflation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Custom DoE screening design
All of the design evaluation information is a function of the design matrix, but the columns for the uncontrolled factors are empty.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us