Correlation between the estimated regression coefficients and correlation between the explanatory variables

[#1]

Hello,

What is the difference between the "correlation between the estimated regression coefficients (corr(b1, b2))" and the "correlation between the explanatory variables (corr(X1, X2))"? I found that, for example, corr(X1, X2) could be positive while corr(b1, b2) is negative. I think I understand corr(X1, X2), but I don't understand why we need to know corr(b1, b2), how it relates to corr(X1, X2), and how we can get those numbers from JMP. Thank you!

[#2]

Try using Analyze> Multivariate Methods> Multivariate.

Throw all your factors and responses into the y role

[#3]

This is an interesting observation: "I found that, for example, corr(X1, X2) could be positive while corr(b1, b2) is negative."

My first reaction is whether this is always true. If not, under what conditions, is this true?

It can be shown that it is always true, excluding singular counter examples, if:

1. There are two explanatory variables
2. The multiple regression has an intercept term,

then the two correlations are exact opposite!

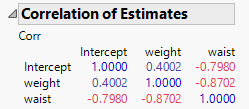
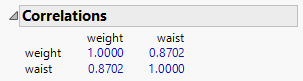
I attach an example. Run the embedded scripts, and here are two screenshots.

Now a little intuition about why so. In this example, CHINS ~ WEIGHT+ WAIST. (I am using all upper case, because I am going to use "weight", all lower case, for separate meaning later.) WEIGHT is positively correlated with WAIST. So large WEIGHT is associated with large WAIST.

But if one uses both to predict CHINS, the prediction is a weighted sum of two number. Adding a little more weight on WEIGHT, while one wants to maintain prediction accuracy, one should subtracting some weight from WAIST. This opposite weight change reflects the meaning of negative correlation of the estimates.

For you questions: why we need to know corr(b1, b2)? We don't, at least not always. One only need to know them in some cases, such as trying to interpret the effects of individual explanatory variables. High correlation may just make things messy.

For the question: how it relates to corr(X1,X2)? My answer is don't bother to establish the relationship in general. It looks interesting for the special situation, but I don't see this can be generalized when there are more than 2 explanatory variables. And relationships will no longer be such clear or consistent.

For the last question, my examples show show.

[#4]

The correlation of the estimates is known as collinearity. It increases the standard errors of the estimates. This, in turn, decreases the power of detecting non-null parameters. It makes interpreting the meaning and assignment of effects to your predictor variables difficult.

The correlation of the estimates is based on the columns in the matrix used to solve for the model parameters with regression analysis. The correlation of the variables has nothing to do with the model.