- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Choice Experiment: where do I fill in prior information? (JMP)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Choice Experiment: where do I fill in prior information? (JMP)
Hi everyone!
A couple of weeks ago, I did a pilot Choice Experiment among 20 consumers in Kenya. Now I would like to use that information as 'priors' for my final Choice Experiment that I'm designing in JMP. However, I'm not sure how/where to fill in which data.
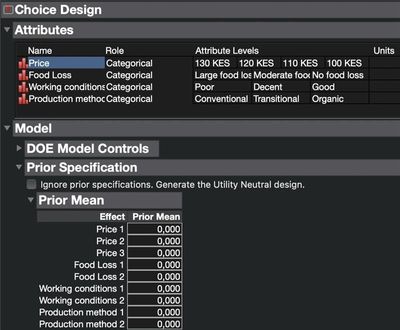
These are my attributes and levels:
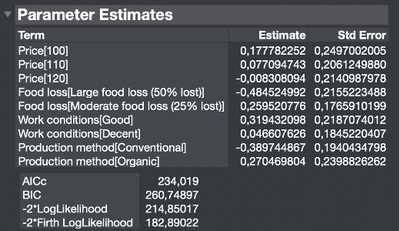
These are the priors (from the pilot study):
But I’m not sure how to fill them in in the final Choice Experiment design. When I want to fill them in in the ‘Prior Mean’ table (see screenshot 3) I don’t know which information to fill in where. For example: where do I fill in the ‘price 100 KES’ estimate of 0,178, does it correspond to price 1, 2 or 3? Maybe it doesn't matter if I fill it in under price 1, 2 or 3?
I'm confused and I hope someone can help me with this :)
Thank you in advance!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Choice Experiment: where do I fill in prior information? (JMP)
Hi @MaFi,
Welcome in the Community :)
You can find an example of a Choice design using prior information in the JMP Help :
Design the Final Choice Experiment Using Prior Information (jmp.com)
And to analyze prior data : Analyze the Pilot Study Data (jmp.com)
For your use case, there are several things to know :
- Depending on the order of the levels for each factor, you'll be able to directly enter the estimate value found before: For example, "Price 2" corresponds in your design to the estimate of "Price[120]" in your initial study, as the level 2 in your new design correspond to level with name "120 KES".
- If you don't have the estimate value directly for a level, you can very simply calculate it. For example, you don't have directly the estimate of Price[130] needed as a prior mean for Price 1 in your new design. No problem, this estimate can be calculated based on the estimates of the other levels, so that the combination of estimates L1 + L2 + L3 + L4 = 0.
So Price[130]has an estimate value of 0 - Price[100] - Price[110] - Price[120] = -0,2465682. - You can also add in your design generation prior variances information if you have the relevant std error estimates needed for the levels in your design; to do this, you need to enter in the diagonal the squared value of your std error estimate (variance = std²) for each corresponding factor level. You need the same ordering in your factors levels between pilot study and choice design study in order to be able to fully complete your diagonale with corresponding factor level variance values.
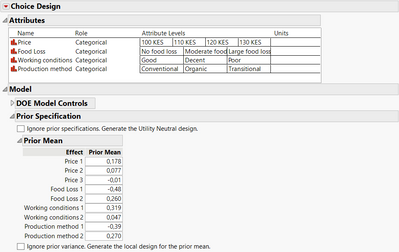
I did the exercice with your data if you want to have a look (but the levels ordering for the factors may be different, so that I can have all parameter estimates and Sdt error estimates values needed (without calculation) for the prior mean and prior variances panels) :
- Enter factors, levels and prior means estimates :
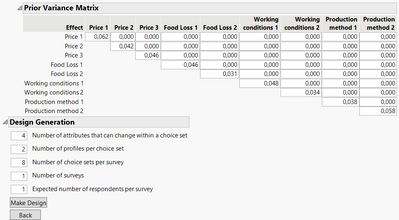
- Calculates prior variances by squaring the values of Std error estimates for each factors levels from the pilot study, and enter prior variances estimates :
You have then to define finally the details for the design generation : number of attributes that can change in a choice set, number of profiles per choice set, etc...
Here is one example script of a generated design :
DOE(
Choice Design,
{Add Factor(
Categorical,
{"100 KES", "110 KES", "120 KES", "130 KES"},
"Price",
0
), Add Factor(
Categorical,
{"No food loss", "Moderate food loss", "Large food loss"},
"Food Loss",
0
), Add Factor(
Categorical,
{"Good", "Decent", "Poor"},
"Working conditions",
0
), Add Factor(
Categorical,
{"Conventional", "Organic", "Transitional"},
"Production method",
0
), Set Random Seed( 10688 ), Add Term( {1, 1} ), Add Term( {2, 1} ),
Add Term( {3, 1} ), Add Term( {4, 1} ),
Set Prior Mean Choice(
[0.1777 0.077 -0.0083 -0.48452 0.2595 0.319 0.0466 -0.3897 0.27]
), Set Prior Variance Matrix(
[0.062 0 0 0 0 0 0 0 0,
0 0.0424 0 0 0 0 0 0 0,
0 0 0.045796 0 0 0 0 0 0,
0 0 0 0.04644025 0 0 0 0 0,
0 0 0 0 0.03118 0 0 0 0,
0 0 0 0 0 0.04783 0 0 0,
0 0 0 0 0 0 0.0340483 0 0,
0 0 0 0 0 0 0 0.0376 0,
0 0 0 0 0 0 0 0 0.05754]
), Set Number of Attributes( 4 ), Set Number of Profiles( 2 ),
Set Number of Choice Sets( 16 ), Set Number of Surveys( 1 ),
Set Expected Number of Respondents( 1 ), Make Design,
Choice Design Table Output( Combined ), Simulate Responses( 0 )}
)And if you're more familiar with datatable, you can find it attached here as well (click on script "DOE Dialog" to change settings in the design generation panel and recreate a new design based on your needs).
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Choice Experiment: where do I fill in prior information? (JMP)
Hi @MaFi,
Welcome in the Community :)
You can find an example of a Choice design using prior information in the JMP Help :
Design the Final Choice Experiment Using Prior Information (jmp.com)
And to analyze prior data : Analyze the Pilot Study Data (jmp.com)
For your use case, there are several things to know :
- Depending on the order of the levels for each factor, you'll be able to directly enter the estimate value found before: For example, "Price 2" corresponds in your design to the estimate of "Price[120]" in your initial study, as the level 2 in your new design correspond to level with name "120 KES".
- If you don't have the estimate value directly for a level, you can very simply calculate it. For example, you don't have directly the estimate of Price[130] needed as a prior mean for Price 1 in your new design. No problem, this estimate can be calculated based on the estimates of the other levels, so that the combination of estimates L1 + L2 + L3 + L4 = 0.
So Price[130]has an estimate value of 0 - Price[100] - Price[110] - Price[120] = -0,2465682. - You can also add in your design generation prior variances information if you have the relevant std error estimates needed for the levels in your design; to do this, you need to enter in the diagonal the squared value of your std error estimate (variance = std²) for each corresponding factor level. You need the same ordering in your factors levels between pilot study and choice design study in order to be able to fully complete your diagonale with corresponding factor level variance values.
I did the exercice with your data if you want to have a look (but the levels ordering for the factors may be different, so that I can have all parameter estimates and Sdt error estimates values needed (without calculation) for the prior mean and prior variances panels) :
- Enter factors, levels and prior means estimates :
- Calculates prior variances by squaring the values of Std error estimates for each factors levels from the pilot study, and enter prior variances estimates :
You have then to define finally the details for the design generation : number of attributes that can change in a choice set, number of profiles per choice set, etc...
Here is one example script of a generated design :
DOE(
Choice Design,
{Add Factor(
Categorical,
{"100 KES", "110 KES", "120 KES", "130 KES"},
"Price",
0
), Add Factor(
Categorical,
{"No food loss", "Moderate food loss", "Large food loss"},
"Food Loss",
0
), Add Factor(
Categorical,
{"Good", "Decent", "Poor"},
"Working conditions",
0
), Add Factor(
Categorical,
{"Conventional", "Organic", "Transitional"},
"Production method",
0
), Set Random Seed( 10688 ), Add Term( {1, 1} ), Add Term( {2, 1} ),
Add Term( {3, 1} ), Add Term( {4, 1} ),
Set Prior Mean Choice(
[0.1777 0.077 -0.0083 -0.48452 0.2595 0.319 0.0466 -0.3897 0.27]
), Set Prior Variance Matrix(
[0.062 0 0 0 0 0 0 0 0,
0 0.0424 0 0 0 0 0 0 0,
0 0 0.045796 0 0 0 0 0 0,
0 0 0 0.04644025 0 0 0 0 0,
0 0 0 0 0.03118 0 0 0 0,
0 0 0 0 0 0.04783 0 0 0,
0 0 0 0 0 0 0.0340483 0 0,
0 0 0 0 0 0 0 0.0376 0,
0 0 0 0 0 0 0 0 0.05754]
), Set Number of Attributes( 4 ), Set Number of Profiles( 2 ),
Set Number of Choice Sets( 16 ), Set Number of Surveys( 1 ),
Set Expected Number of Respondents( 1 ), Make Design,
Choice Design Table Output( Combined ), Simulate Responses( 0 )}
)And if you're more familiar with datatable, you can find it attached here as well (click on script "DOE Dialog" to change settings in the design generation panel and recreate a new design based on your needs).
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Choice Experiment: where do I fill in prior information? (JMP)
Hi Victor,
Thank you very much for your help, that was exactly what I needed to be able to continue :)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us