- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- CCD : Uniform Precision + Rotatable
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
CCD : Uniform Precision + Rotatable
Hi,
In DOE RSM, we have few choices to choose from. One of it is Uniform Precision.
I understand this design provides constant prediction error within the design space (-1 to +1), hence the name Uniform Precision.
However, there is then options to choose for a Rotatable property. I understood Rotatable means, the prediction error is constant for any points equidistant from the center point.
My question is :
Is there any benefit for choosing a combination of Uniform Precision + Rotatable, since it seems the Rotatable property is redundant as the Uniform Precision is already providing the constant prediction error.
Thanks for advise.
B.r,
Chris Looi
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CCD : Uniform Precision + Rotatable
Uniform precision does not really give constant prediction error from -1 to +1. You can see this by using Design Evaluation in JMP to look at the prediction variance of a uniform precision design. It is, of course, very low and flat for a large proportion of the design space.
Rotatability might seem like it adds no advantage, but that is not the case. Rotatability is achieved by setting the axial points at a certain level. This improves the prediction variance throughout the design space.
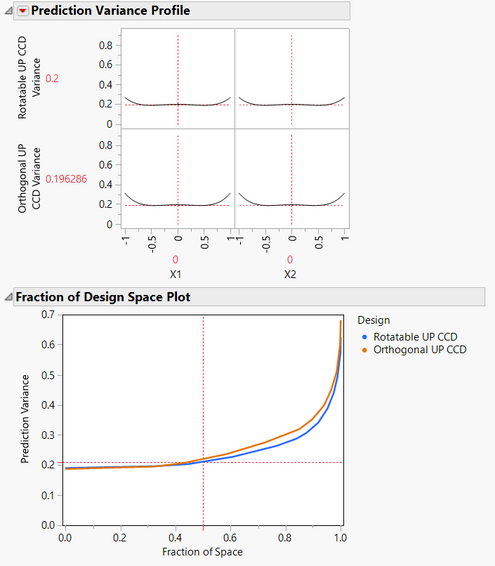
To illustrate, I created a 2 factor rotatable uniform precision CCD (5 center points) and a 2 factor orthogonal CCD with 5 center points. The ortogonal CCD will use a different axial distance. I then used the Compare Designs platform in JMP. Look at the prediction variance profile and fraction of design space plot. Although the designs are similar, the rotatable CCD performs better in terms of prediction variance.
Is this enough to worry about? Maybe not, but this difference is even more extreme when compared to an on-face central composite design, which it seems most people use (if using a central composite design).
Ultimately, the choice of the axial levels does have some impact on the prediction variance and the power of the design. Practicality does usually trump these mathematical considerations, but there are mathematical differences.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CCD : Uniform Precision + Rotatable
I guess in addition to having equal variance at anypoint at a given radius, you would also have relatively equal variance for any points within the design space circle/sphere/hypershpere? It will just try to further flatten the prediction variance surface in addition to being rotatable.
In my opinion, it's only of academic interest. Practically, the exact value of the axials makes little difference and is usually driven more by what levels of precision you can actually achieve in setting those factors anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CCD : Uniform Precision + Rotatable
Uniform precision does not really give constant prediction error from -1 to +1. You can see this by using Design Evaluation in JMP to look at the prediction variance of a uniform precision design. It is, of course, very low and flat for a large proportion of the design space.
Rotatability might seem like it adds no advantage, but that is not the case. Rotatability is achieved by setting the axial points at a certain level. This improves the prediction variance throughout the design space.
To illustrate, I created a 2 factor rotatable uniform precision CCD (5 center points) and a 2 factor orthogonal CCD with 5 center points. The ortogonal CCD will use a different axial distance. I then used the Compare Designs platform in JMP. Look at the prediction variance profile and fraction of design space plot. Although the designs are similar, the rotatable CCD performs better in terms of prediction variance.
Is this enough to worry about? Maybe not, but this difference is even more extreme when compared to an on-face central composite design, which it seems most people use (if using a central composite design).
Ultimately, the choice of the axial levels does have some impact on the prediction variance and the power of the design. Practicality does usually trump these mathematical considerations, but there are mathematical differences.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: CCD : Uniform Precision + Rotatable
That's a good point there are huge advantages over on-face axials. At that point, the CCD has no advantage over I-optimal RSMs of the same size, so I never even consider CCDs at that point. Off-face or bust!
In truth though, the levels that correspond to those precise axial values for rotatability and orthogonality are often not viable due to resolution levels for those process knobs. If you find something close, you might be able to split the difference between those options. In the end, you're still probably doing a lot better than an on-face CCD, which is a good design anyway, so you can't really go wrong.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us