- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Blocks and Center points for a definitive screening design
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Blocks and Center points for a definitive screening design
I began to create a definitive screening design with 7 factors and 3 response varianbles with JMP. I set "no blocks"!. Why is the number of blocks shown below equal to 2? I wanted to add only 2 centre point measurements. Is "Einzelversuche" equal to replicates? Why can I only add 4 additional measurements? I can only set to zero "Einzelversuche" and number of blocks ("Anzahl Blöcke") cannot be changed at all. Why?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
Hi @Thommy7571,
Dadurch wird die Attraktivität von DSDs vermindert, die ja schon ohne weitere Messungen in der Lage sein sollen, quadratische Effekte und Wechselwirkungen zwischen den Haupteffekten zu trennen. Andererseits hatte ChatGPT mir auch vorgeschlagen.mehrere Zentralpunktmessungen hinzuzufügen, so wie es MathStatChem geschrieben hatte. Bradley hatte das Thema nicht näher in seinem DSD Artikel behandelt. Der genaue Effekt und zitierfähige Gründe dafür liegen mir daher nicht vor. Gibt es einen Artikel, indem der Effekt unterschiedlicher Anzahlen von hinzugefügten Zentralpunkt-messungen und / oder Blöcken mit Zentralpunktmessungen untersucht wird?
Again, I would avoid using ChatGPT for precise answers, particularly on modern designs like DSD. The responses may be highly generic, and not particularly suited for your specific use case, or the use of DSDs.
Concerning the effect of adding centre points or extra runs, you can search for publications or try several scenarii in JMP, by creating several designs and compare them. I created 3 DSDs for this scenario :
- DSD for 7 continuous factors, minimum amount of runs required (17 runs).
- DSD for 7 continuous factors, 21 runs with 5 centre points (1 created by default, 4 added in the datatable after)
- DSD for 7 continuous factors, 21 runs with 4 extra runs.
Here are the main differences :
- Power analysis
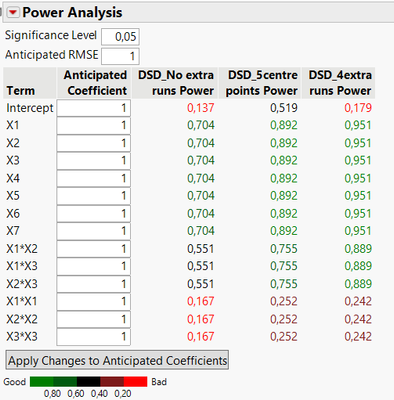
With the model specified here (assuming 3 interactions and 3 quadratic effects), you can see that both "augmented" DSD designs (with 21 runs) have increased power to detect main effects, interactions, and quadratic effects. The difference is :
- DSD with added centre points has a slightly higher power to detect quadratic effects, but the gain on detecting interactions is not very high compared to the situation with 4 extra runs.
- DSD with 4 extra runs has similar power to detect quadratic effects and higher power for detecting 2-factors interactions. This is due to the fact that extra runs are not replicates runs (unlike centre points which correspond to the same setting/treatment) and DSD runs have factors set to 3 levels, so extra runs do significantly improve power for main effects, interactions and are able to increase power for quadratic effects as well.
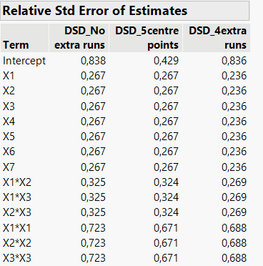
Looking at relative standard error of estimates for the assumed model, you have the same interpretation than with power analysis : adding centre points only improve significantly the precision to estimate quadratic effects (and intercept), whereas adding extra runs enable to improve the precision to estimate terms more uniformly.
- Prediction variance
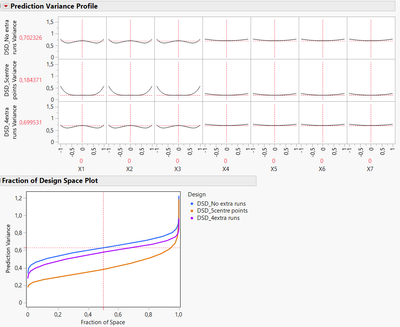
In terms of prediction variance, centre points enable to have a lower and more stable prediction variance in the centre of the experimental space. This can be particularly useful if you think your optimum point may be in the centre of the experimental space. However, DSD with only centre points tend to have a prediction variance higher in the corners of the experimental, since all added points are centre points which only decrease prediction variance around the centre of your experimental space :
You can see here by maximizing prediction variance, the DSD with 5 centre points has a prediction variance close from the "non-augmented" original DSD, whereas DSD with 4 extra runs enable to reduce prediction variance more homogeneously at the borders of your experimental space.
- Efficiencies :
You can see that DSD with 4 extra runs has better D and G-efficiencies (the comparison reference is the original 17 runs DSD, so the lower the relative efficiency of the original DSD with another DSD, the better the gain for this other DSD). Little reminder about efficiencies here : Design Diagnostics (jmp.com) and https://en.wikipedia.org/wiki/Optimal_experimental_design
So having better relative D-Efficiency is useful in the screening stage, as this enable to have a better precision in the estimation of effect terms. G-Efficiency may also be useful, as it enables to minimize the maximum prediction variance, so to have a prediction variance more homogeneous between the centre of the experimental space and the borders.
Relatives A-efficiency, focused on minimizing the average variance of the regression coefficients, and I-efficiency, focused on minimizing the average prediction variance over the experimental space, are slightly better in the design with 5 centre points than in the design with 4 extra runs.
Sind DSDs für 7 Faktoren erfahrungsgemäß noch gut brauchbar?
If you have continuous factors, I would highly recommend using DSD for an efficient screening for 5+ factors. You can always check if this design seems useful for you, by creating DSD and other screening designs (classical screening designs with Hadamard matrices, D-/A-Optimal designs, ...) and use the platform Compare Designs (jmp.com). Take into consideration that most screening designs only have 2 levels for the factors, unlike DSDs.
Unklar ist, was jetzt "Fake factors" sein sollen.
"Fake factors" are factors added in the creation of the DSD to generate a higher number of runs in the design, but that have no practical interest: they are not linked to a specific experimental factor you want to change, simply here to increase the matrix size. Adding runs with "fake factors" is a trick to enable better effects estimation and increased power, and also increase degree of freedoms available to fit additional terms in the model.
Some ressources to help you on understanding DSDs :
Introducing Definitive Screening Designs - JMP User Community
Definitive Screening Design - JMP User Community
The Fit Definitive Screening Platform (jmp.com)
Using Definitive Screening Designs to Get More Information from Fewer Trials - JMP User Community
And more generally on DoEs :
DoE Resources - JMP User Community
I added the three designs generated as an example if you want to reproduce the analysis and comparison.
Hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
Hi @Thommy7571,
If you have selected the option "No Block" in the DSD platform, the created design won't have any block.
The values you see are only "default" options that are activated if you select one of the options ("Block with centre runs" or "Block without centre runs").
By default, JMP create a centre run in the DSD, and will create blocks if you want several centre runs (one centre run / block). But you can always edit your datatable to add an additional centre run if needed.
Yes, extra runs are equivalent to replicates (independent runs), but they are not exactly replicates : they are created using "fake factors", so you may not have the same factor values as for other runs of the design. Extra Runs can be added by block of four : you can add 4 or 8 extra runs in your design, so you can change the setting to 0 (no extra runs), 4 or 8 extra runs. You may find additional information about the specific structure of DSDs here : Structure of Definitive Screening Designs
On my computer, I can increase the number of blocks, and this change the setting from "No Block" to "Add Blocks with Center Runs to Estimate Quadratic Effects" :
Hope this will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
You can go ahead and create the design, and it will not add blocks. By default the DSD generator adds 4 center points, but you can choose only use 2 center points, just delete two of the center point runs in the generated design. The reason that 4 center points is the default is that some research showed that the power to detect important effects is much less with 2 center points vs 4 center points.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
The "Extra Runs" are not centre points.
By default, without any block, a DSD will include one centre point in JMP. Adding block enable to add centre points (one centre point for each block).
The default 4 extra runs are used to better detect interactions and quadratic effects, as well as increasing power for main effects :
Since these runs are not replicates, they also provide additional degree of freedoms to detect and estimate more effect terms.
Hope this answer solves any ambiguity,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
Hallo,
<<<Zusätzliche Läufe können in Viererblöcken hinzugefügt werden: Sie können 4, 8 etc. Messungen hinzufügen, pro Block ein Zentralpunkt
ok, ich fasse zusammen: Es können (vermutlich) beliebig viele Blöcke hinzugefügt werden (also +4, +8, etc.) Es kann eine Zentralpunktmessung pro Block mit 4 Messungen hinzugefügt werden.
Das ist einerseits ungünstig, weil das die Anzahl der Messungen des DSD stark erhöht. Dadurch wird die Attraktivität von DSDs vermindert, die ja schon ohne weitere Messungen in der Lage sein sollen, quadratische Effekte und Wechselwirkungen zwischen den Haupteffekten zu trennen. Andererseits hatte ChatGPT mir auch vorgeschlagen.mehrere Zentralpunktmessungen hinzuzufügen, so wie es MathStatChem geschrieben hatte. Bradley hatte das Thema nicht näher in seinem DSD Artikel behandelt. Der genaue Effekt und zitierfähige Gründe dafür liegen mir daher nicht vor. Gibt es einen Artikel, indem der Effekt unterschiedlicher Anzahlen von hinzugefügten Zentralpunkt-messungen und / oder Blöcken mit Zentralpunktmessungen untersucht wird?
Sind DSDs für 7 Faktoren erfahrungsgemäß noch gut brauchbar?
Unklar ist, was jetzt "Fake factors" sein sollen.
Thommy7571
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
Hi @Thommy7571,
Dadurch wird die Attraktivität von DSDs vermindert, die ja schon ohne weitere Messungen in der Lage sein sollen, quadratische Effekte und Wechselwirkungen zwischen den Haupteffekten zu trennen. Andererseits hatte ChatGPT mir auch vorgeschlagen.mehrere Zentralpunktmessungen hinzuzufügen, so wie es MathStatChem geschrieben hatte. Bradley hatte das Thema nicht näher in seinem DSD Artikel behandelt. Der genaue Effekt und zitierfähige Gründe dafür liegen mir daher nicht vor. Gibt es einen Artikel, indem der Effekt unterschiedlicher Anzahlen von hinzugefügten Zentralpunkt-messungen und / oder Blöcken mit Zentralpunktmessungen untersucht wird?
Again, I would avoid using ChatGPT for precise answers, particularly on modern designs like DSD. The responses may be highly generic, and not particularly suited for your specific use case, or the use of DSDs.
Concerning the effect of adding centre points or extra runs, you can search for publications or try several scenarii in JMP, by creating several designs and compare them. I created 3 DSDs for this scenario :
- DSD for 7 continuous factors, minimum amount of runs required (17 runs).
- DSD for 7 continuous factors, 21 runs with 5 centre points (1 created by default, 4 added in the datatable after)
- DSD for 7 continuous factors, 21 runs with 4 extra runs.
Here are the main differences :
- Power analysis
With the model specified here (assuming 3 interactions and 3 quadratic effects), you can see that both "augmented" DSD designs (with 21 runs) have increased power to detect main effects, interactions, and quadratic effects. The difference is :
- DSD with added centre points has a slightly higher power to detect quadratic effects, but the gain on detecting interactions is not very high compared to the situation with 4 extra runs.
- DSD with 4 extra runs has similar power to detect quadratic effects and higher power for detecting 2-factors interactions. This is due to the fact that extra runs are not replicates runs (unlike centre points which correspond to the same setting/treatment) and DSD runs have factors set to 3 levels, so extra runs do significantly improve power for main effects, interactions and are able to increase power for quadratic effects as well.
Looking at relative standard error of estimates for the assumed model, you have the same interpretation than with power analysis : adding centre points only improve significantly the precision to estimate quadratic effects (and intercept), whereas adding extra runs enable to improve the precision to estimate terms more uniformly.
- Prediction variance
In terms of prediction variance, centre points enable to have a lower and more stable prediction variance in the centre of the experimental space. This can be particularly useful if you think your optimum point may be in the centre of the experimental space. However, DSD with only centre points tend to have a prediction variance higher in the corners of the experimental, since all added points are centre points which only decrease prediction variance around the centre of your experimental space :
You can see here by maximizing prediction variance, the DSD with 5 centre points has a prediction variance close from the "non-augmented" original DSD, whereas DSD with 4 extra runs enable to reduce prediction variance more homogeneously at the borders of your experimental space.
- Efficiencies :
You can see that DSD with 4 extra runs has better D and G-efficiencies (the comparison reference is the original 17 runs DSD, so the lower the relative efficiency of the original DSD with another DSD, the better the gain for this other DSD). Little reminder about efficiencies here : Design Diagnostics (jmp.com) and https://en.wikipedia.org/wiki/Optimal_experimental_design
So having better relative D-Efficiency is useful in the screening stage, as this enable to have a better precision in the estimation of effect terms. G-Efficiency may also be useful, as it enables to minimize the maximum prediction variance, so to have a prediction variance more homogeneous between the centre of the experimental space and the borders.
Relatives A-efficiency, focused on minimizing the average variance of the regression coefficients, and I-efficiency, focused on minimizing the average prediction variance over the experimental space, are slightly better in the design with 5 centre points than in the design with 4 extra runs.
Sind DSDs für 7 Faktoren erfahrungsgemäß noch gut brauchbar?
If you have continuous factors, I would highly recommend using DSD for an efficient screening for 5+ factors. You can always check if this design seems useful for you, by creating DSD and other screening designs (classical screening designs with Hadamard matrices, D-/A-Optimal designs, ...) and use the platform Compare Designs (jmp.com). Take into consideration that most screening designs only have 2 levels for the factors, unlike DSDs.
Unklar ist, was jetzt "Fake factors" sein sollen.
"Fake factors" are factors added in the creation of the DSD to generate a higher number of runs in the design, but that have no practical interest: they are not linked to a specific experimental factor you want to change, simply here to increase the matrix size. Adding runs with "fake factors" is a trick to enable better effects estimation and increased power, and also increase degree of freedoms available to fit additional terms in the model.
Some ressources to help you on understanding DSDs :
Introducing Definitive Screening Designs - JMP User Community
Definitive Screening Design - JMP User Community
The Fit Definitive Screening Platform (jmp.com)
Using Definitive Screening Designs to Get More Information from Fewer Trials - JMP User Community
And more generally on DoEs :
DoE Resources - JMP User Community
I added the three designs generated as an example if you want to reproduce the analysis and comparison.
Hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
Thanks very much for this study. Just some remarks. According to Bradly, the minimum is 15 runs for 7 factors, except the design should be orthogonal, what will be the case with 17 runs. It is interesting to see that the factorial points are included - as I already considered. Thus, corner points are also better included. I just reread the article and taking 8 factors for the design eliminating the last column afterwards should correspond to your suggestion. The results are quite logic - mor replicates in a given reagion higher reliability of the prediction in the region I will give up ChatGPT concerning designs... There was the suggestion to use an A optimal design as standard (one video of the links of your last answers). That is why I also targetted it. Should I change to G-optimal for the screening? Why?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Blocks and Center points for a definitive screening design
Hi @Thommy7571,
According to Bradly, the minimum is 15 runs for 7 factors, except the design should be orthogonal, what will be the case with 17 runs.
Sorry, but the information about the minimum number of runs is incomplete. The complete information about required minimum number of runs can be accessed here : Structure of Definitive Screening Designs
To summarize the content :
- If you have a k even number of continuous factors, you need 2k+1 runs
- If you have a k uneven number of continuous factors, you need 2k+3 runs
So for 7 factors, you need a minimum of 17 runs, and for 8 factors the minimum is also 17. This run size is a specificity of DSD also mentioned and discovered by members of this Community, for example in this post : https://community.jmp.com/t5/Discussions/Verify-and-use-existing-Definitive-Screen-design-with-JMP/m...
You can also verify this using the Definitive Screening Designs platform and generating designs for different number of factors. Note that this rule depends on the existence of a conference matrix of the required size, see an example here : Solved: Re: 49 factor dsd design - JMP User Community
I just reread the article and taking 8 factors for the design eliminating the last column afterwards should correspond to your suggestion.
Yes, to add extra runs, you can add "fake" factors and then remove their columns ; this is how the extra runs are generated in the DSD platform.
There was the suggestion to use an A optimal design as standard (one video of the links of your last answers). That is why I also targetted it. Should I change to G-optimal for the screening? Why?
D- and A- optimality criterion are more targeted for screening designs, as they focus on precise estimation or variance reduction of the coefficients estimates, so it enables to more efficiently screen and filter out non-important from important factors, based on statistical significance, to be confirmed with practical significance and domain expertise.
Bradley Jones emphasizes indeed the use of A-Optimal designs for screening, as they enable similar (if not better) performances than D-Optimal screening designs, and also enable to add different emphasis on the estimation of some terms (for example give more importance/weight for the precise estimation of main effects instead of interactions) : 21st Century Screening Designs (2020-US-45MP-538)
G- and I- optimality criterion are more targeted for response surface model designs, where the focus is on predictive performance over the experimental space to enable optimization. G-optimality criterion focus and minimize the maximum prediction variance, whereas I-optimality minimize the average prediction variance.
Hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us