How do I test not only for differences among slopes, but also that the slopes are different from zero (significant) in a linear mixed effects model with 1 continuous and 1 categorical (2 level) variables, and two random effects.
In the Parameter Estimates output below I see that I have a significant interaction between tissue type [MSC] and lnSe. Meaning that the slope for MSC is different from the baseline value. BUT, is the actual slope of MSC different from zero?? How do I test that within the mixed model? Clearly I can run a simple regression, but I want to control for random effects in the mixed model.
I'm using JMP13, Fit model platform.
Thanks!
Community Manager
Hi @arstewar,
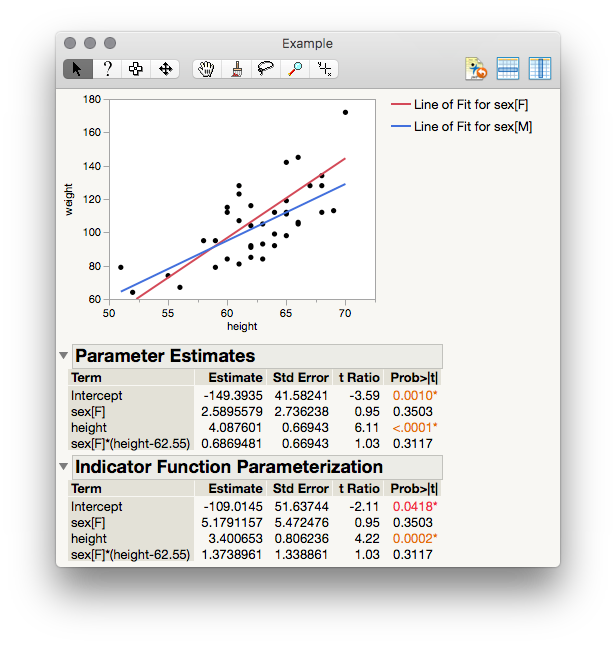
There are a few ways to go about this, but I think the most direct will be to use the indicator variable parameter tests. Select under the top Red Triangle > Estimates > Indicator Parameterization Estimates to reveal that table. The example below is using Big Class with Sex, Height, and Sex * Height as model effects, predicting Weight. Not a random effect model, but the same logic applies and can be extended for this particular test.
The original parameter estimates table shows parameter effects and tests with respect to the grand mean, which is the consequence of "effect coding" of our nominal terms. That also means, when a continuous regressor is involved, that the slope (of height in this case) is the average slope between men and women of weight on to height, and to find the slope for either males or females you would either subtract or add the interaction coefficient. For example, to find the slope for men using the original parameter estimates table, we take the reported slope for height, then subtract the interaction coefficient (which is the offset, or effect, on the average slope for males): 4.0876 - 0.6869 = 3.4007.
Now let's look at the Indicator Function table. The reported coefficient of height here will not be the average between men and women; rather, it will be the slope for just one level of your categorical factor. In this case, it will be the males, since M is after F and unless we set value ordering the last level alphabetically is used as the "control." So, we should expect to find as the coefficient for height in the Indicator Function Parameterization table the same value we just calculated, and indeed, 3.400653 is reported.
Now, to your question about tests. The reported p-values here are testing coefficients in either table against a null of 0. So, if we are interested in whether the slope for men is equal to 0, we can simply look in the Indicator Function Parameterization table at the row for height. In this case, we reject the null, t=4.22, p = 0.0002. If we were interested in testing the slope for women instead, we would need to change the value ordering for our column in Column Info, then rerun the analysis. In essence, that's what the add-in I have on the community does for testing simple slopes in a one-way ancova-like model. The fact there are random effects in the model doesn't change anything with respect to this test since JMP is smart enough to know how to calculate the standard errors for these coefficients in all cases.
I hope this helps!