- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Are statistically different two linear regression?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Are statistically different two linear regression?
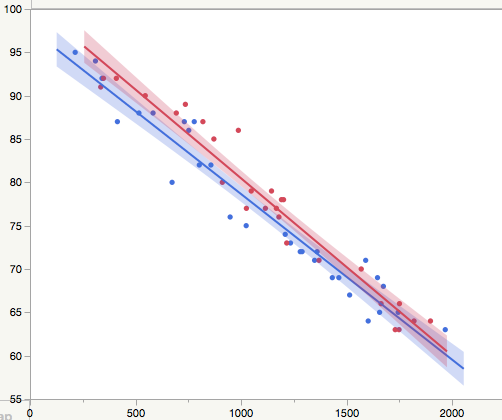
Can somone help me to understand when two linear regression are statistically different?
In the picture below, my situation. Blu and Red lines corrisponding at two set of data by two different process. How I can understand if the regression are statistically different or not? in other word the two process give are equal, then doens't have impact on the results?
Thanks in advance.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
The way to do this is to fit a single model to both datasets.
Stack your two datasets so that you will have columns Y, X, Color (which is either blue or red),
Now using Fit Model, specify the model y = b0 + b1*X + b2*Color + b12*X*Color.
When analyzing the results, if the b2 parameter estimate is significant, then the intercepts for the two models are different. If the b12 parameter estimate is significant, then the two models have different slopes.
The interpretation is such that if you fix the color, then b2 is just an adjustment to the intercept and b12 is just an adjustment to the slope of X. Therefore, the testing of those parameter estimates is equivalent to saying are the intercepts and slopes different, respectively.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
Just to clarify the approach described by Dan. It is a form of hypothesis testing. It assumes that there is no difference (null hypothesis) so a significant test finds in favor of a difference (alternative hypothesis). If you are tasked with demonstrating equivalence, then the hypotheses are reversed.
Hypothesis tests are work in one direction. A test for a difference that is not significant is not the same as a significant test for equivalence.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
Dan and Mark answered your question, this is just a recommendation to look at the residuals for each model fit versus the X values.
Both blue and red independent regression fit lines residuals appear to be "high" (above their respective lines) when X is near 500. They do not look random. A final note is that all statistical comparative methods have built-in assumptions (random residuals, independence, etc.) and of course most important, were the data collected in such a way that that the comparison is fair.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
Dan and Mark have both answered this but in the spirit of the discussion I just wanted to provide some slightly different language.
You have two models red and blue and you have asked if the two models are statistically significant.
So first we have to think about what you mean by that question.
The models could differ in that the red and blue lines have different slopes. Clearly the slopes are slightly different, but is the difference statistically significant? To answer that question we build a model that contains an interaction term, what I think Dan has referred to as X*Color. This term allows the effect of X to depend on the colour.
(As a side note, addressed by Dan, in order to have X and Color in the model we have to have these data represented as column variables, hence the need to stack the data).
Once I have a model with an X*Color term then I can check to see whether that parameter estimate is statistically signicant.
The two lines can also be offset from each other (i.e. in addition to checking whether slope depends on Color we can check to see whether the intercept depends on Color). For this the model needs a term for Color (as well as X). Ultimately then the model we want to build is:
Y = b0 + b1.X + b2.Color + b3.X*Color
the p-value for b3 tells us whether or not the difference in slopes is statistically significant between colours; the p-value for b2 tells us whether the difference in intercepts is statistically significant.
You might also want to do a google search for "analysis of covariance"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
I reiterate: Don't forget to perform a residual analysis, recall the Anscombe dataset. Attached is a data table with 3 scripts:
- Fits a covariance model (interaction b12 * X * Color)
- Fits independent models drawn on the same graph
- Fits independent models drawn on two side-by-side graphs (shown below)
The slopes intercepts, RSquare and RMSE are essentially the same, however Blue is not a good fit.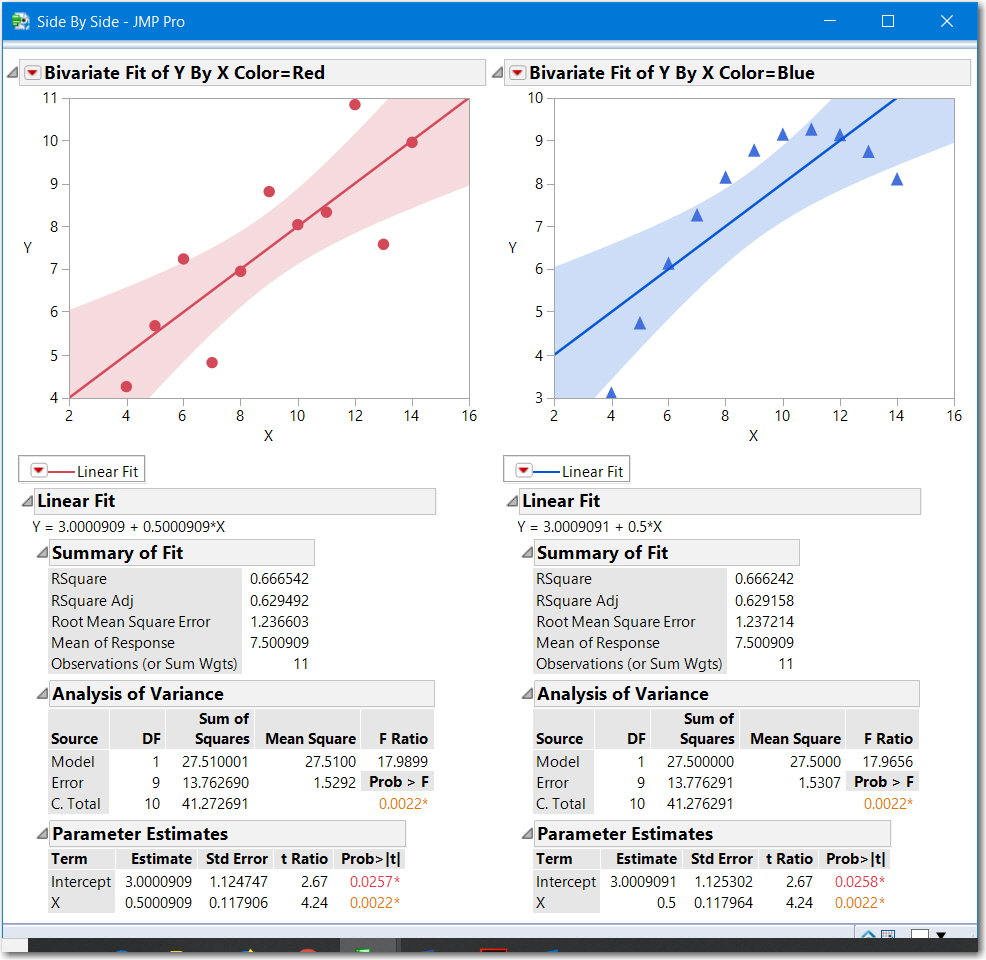
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
The way to do this is to fit a single model to both datasets.
Stack your two datasets so that you will have columns Y, X, Color (which is either blue or red),
Now using Fit Model, specify the model y = b0 + b1*X + b2*Color + b12*X*Color.
When analyzing the results, if the b2 parameter estimate is significant, then the intercepts for the two models are different. If the b12 parameter estimate is significant, then the two models have different slopes.
The interpretation is such that if you fix the color, then b2 is just an adjustment to the intercept and b12 is just an adjustment to the slope of X. Therefore, the testing of those parameter estimates is equivalent to saying are the intercepts and slopes different, respectively.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
Just to clarify the approach described by Dan. It is a form of hypothesis testing. It assumes that there is no difference (null hypothesis) so a significant test finds in favor of a difference (alternative hypothesis). If you are tasked with demonstrating equivalence, then the hypotheses are reversed.
Hypothesis tests are work in one direction. A test for a difference that is not significant is not the same as a significant test for equivalence.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
Dan and Mark answered your question, this is just a recommendation to look at the residuals for each model fit versus the X values.
Both blue and red independent regression fit lines residuals appear to be "high" (above their respective lines) when X is near 500. They do not look random. A final note is that all statistical comparative methods have built-in assumptions (random residuals, independence, etc.) and of course most important, were the data collected in such a way that that the comparison is fair.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
Dan and Mark have both answered this but in the spirit of the discussion I just wanted to provide some slightly different language.
You have two models red and blue and you have asked if the two models are statistically significant.
So first we have to think about what you mean by that question.
The models could differ in that the red and blue lines have different slopes. Clearly the slopes are slightly different, but is the difference statistically significant? To answer that question we build a model that contains an interaction term, what I think Dan has referred to as X*Color. This term allows the effect of X to depend on the colour.
(As a side note, addressed by Dan, in order to have X and Color in the model we have to have these data represented as column variables, hence the need to stack the data).
Once I have a model with an X*Color term then I can check to see whether that parameter estimate is statistically signicant.
The two lines can also be offset from each other (i.e. in addition to checking whether slope depends on Color we can check to see whether the intercept depends on Color). For this the model needs a term for Color (as well as X). Ultimately then the model we want to build is:
Y = b0 + b1.X + b2.Color + b3.X*Color
the p-value for b3 tells us whether or not the difference in slopes is statistically significant between colours; the p-value for b2 tells us whether the difference in intercepts is statistically significant.
You might also want to do a google search for "analysis of covariance"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Are statistically different two linear regression?
I reiterate: Don't forget to perform a residual analysis, recall the Anscombe dataset. Attached is a data table with 3 scripts:
- Fits a covariance model (interaction b12 * X * Color)
- Fits independent models drawn on the same graph
- Fits independent models drawn on two side-by-side graphs (shown below)
The slopes intercepts, RSquare and RMSE are essentially the same, however Blue is not a good fit.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us