- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Applying kernel smoothing to large datasets
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Applying kernel smoothing to large datasets
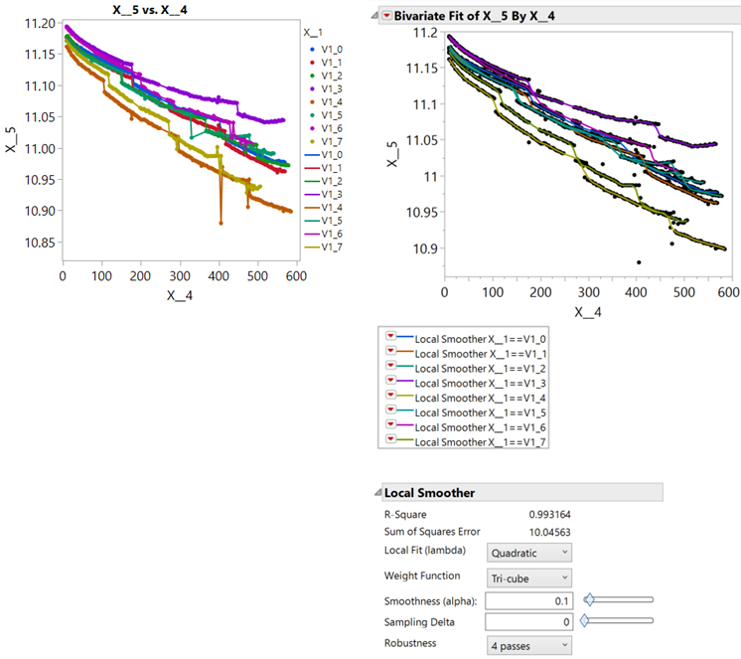
I frequently work with time series data acquired simultaneously from multiple sensors. For example, 100 sensors may make measurements once per hour for several months. The sensors sometimes report erroneous values and sometimes fail to report. I want to remove the outliers from the dataset and impute the missing values in order to extract values from specific points in time for further post-processing and analysis. The kernel smoother in the bivariate platform, with one or more robustness passes, does an excellent job with the fitting. However, I've been unable to effectively apply to a large dataset (hundreds of sensors).
As an example, a representative datatable has 3 columns: Sensor ID, Time, and Measurement. Is there an effective way to replace the values in the Measurement column with the kernal smoothed values based on a fit of Measurement vs Time by Sensor ID?
The solution described here is an elegant way to impute missing values, but a spline fit is either influenced too strongly by the outliers (small lambda) or too stiff to respond to the real curvature in the data (large lambda) and I do not see how to access the kernel smoother objects in the scripting index. Charts of anonymized data (raw data on left, smoother applied on right) are pasted below and the datatable from which they were generated is attached.
-Will
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Applying kernel smoothing to large datasets
I attached an (old) script that implements most of Cleveland's LOESS estimator options. It does not support By groups but you could adapt it.
Also, did you try to save the summaries from from the fit in the FDE? One choice is to save the formulas. The conditional prediction formula will provide a function prediction for any time value - no gaps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Applying kernel smoothing to large datasets
Do you have JMP Pro 14? If so, you might investigate Analyze > Specialized Modeling > Functional Data Explorer.
Also, I assume that in your example, each function would be a smooth curve except for random noise. It also exhibits, though, spurious results (outliers) and a sudden change for a new period of time. Can you distinguish between real signal and anomaly or bias?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Applying kernel smoothing to large datasets
Mark,
Thank you for responding quickly.
I do have JMP Pro 14 and have done some work with the functional data explorer, including cleaning data and fitting b splines. I've made use of the tools that assist in manual cleaning of data and found them to work well in some cases. In the use case that I described however, there are a 3 items that I am looking to workaround.
1. It takes considerable time to clean a large dataset in FDE (hundreds of individual time series)- manually zooming into each time series, selecting points, clicking "remove"....
2. The predicted time series that are output from the fitted splines in FDE do not impute missing data. For example, if the data for time = 1000 was missing from the original dataset, it is missing from the fit. If there is an effective way to impute the values directly in FDE, I have not found it. I can find a workaround for this by inserting the missing time values, fitting a spline and using the calculated spline values. I'd like to eliminate the extra steps.
3. I'd ultimately like to do the smoothing "in-place", with a script that replaces the raw data with smoothed data on a datatable that might contain several hundred sensors, each with several hundred datapoints.
Distinguising between real signal and anomaly or bias is relatively straightforward in the dataset, with knowledge of how it is generated. The step type changes are real, but the spurious single points are miscalculated values. The spurious datapoints in the datasets typical of this analysis (which I execute several times per week) are very easily detected by eye. Also, a LOESS smoother reliably identifies them.
-Will
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Applying kernel smoothing to large datasets
I attached an (old) script that implements most of Cleveland's LOESS estimator options. It does not support By groups but you could adapt it.
Also, did you try to save the summaries from from the fit in the FDE? One choice is to save the formulas. The conditional prediction formula will provide a function prediction for any time value - no gaps.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Applying kernel smoothing to large datasets
Thanks for the script and for pointing me to the conditional prediction formula.
-Will
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Applying kernel smoothing to large datasets
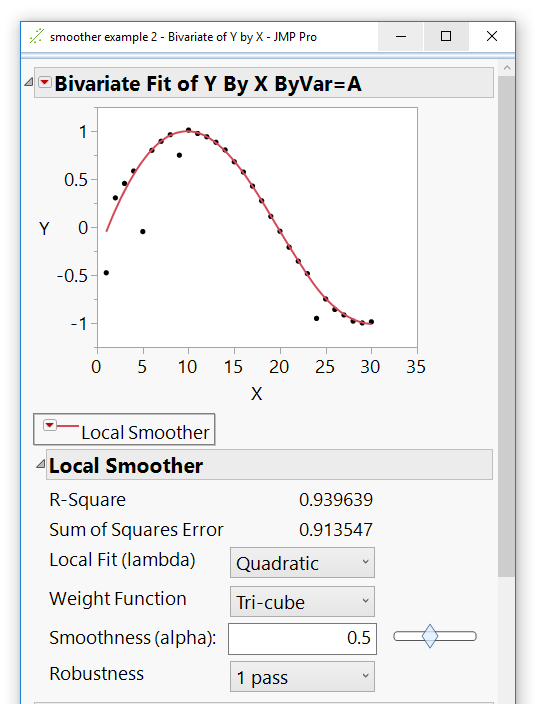
I was able to figure out how to access the kernel smoother in the bivariate platform. A script that creates some fake noisy data, fits a kernel smoother to the data (with a by variable) and saves the fit to a new column in the data table is below
dt = New Table( "smoother example",
Add Rows( 90 ),
New Column( "X",
Numeric,
"Continuous",
Format( "Best", 12 ),
Set Values(
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28,
29, 30, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18,
19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]
)
),
New Column( "Y",
Numeric,
"Continuous",
Format( "Best", 12 ),
Formula(
Sine( :X / (Pi() * 2) ) + Random Normal( 0, 0.01 ) + (
Floor( Random Uniform( 0, 10 ) ) == 1) * Random Uniform( -1, 1 )
),
Set Display Width( 100 )
),
New Column( "ByVar",
Character,
"Nominal",
Set Values(
{"A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A",
"A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A", "A",
"A", "A", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B",
"B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B", "B",
"B", "B", "B", "B", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C",
"C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C", "C",
"C", "C", "C", "C", "C", "C"}
)
)
);
obj = dt << Bivariate(
Ignore Platform Preferences( 1 ),
Y( :Y ),
X( :X ),
By( :ByVar )
);
obj << Kernel Smoother( 2, 1, 0.5, 1 );
obj << (curve[1] << save predicteds);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Applying kernel smoothing to large datasets
Nice example!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us