Reed–Muench method는 Biological procedure에서 endpoint를 결정하는 가장 단순하면서도 직관적인 방법입니다.
위 방법론은 1937년 The American Journal of Hygiene에 발표된 "A Simple Method of Estimating Fifty Per Cent Endpoints"라는 논문에 설명되어 있는 방법론입니다.
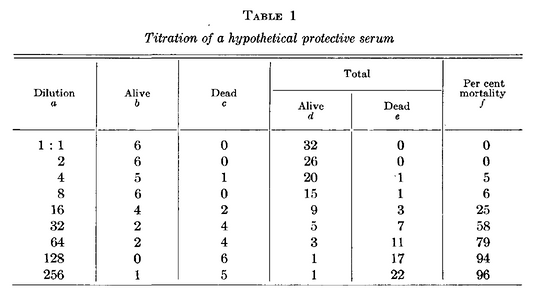
논문에 제시된 데이터를 JMP Data Table로 만듭니다. 논문의 Table 1에 해당되는 데이터에서 Dilution에 해당되는 데이터는 Log 변환을 통해 수치화합니다.
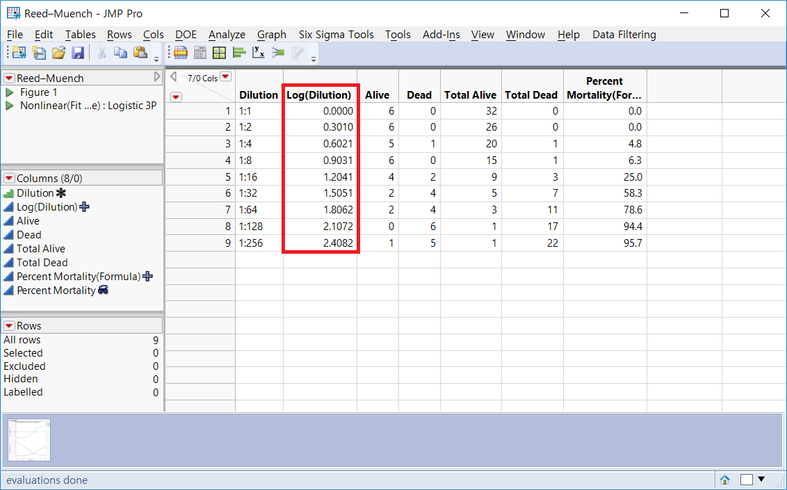
위 빨간 박스의 Log(Dilution)이라는 변수를 만들기 위해선 아래와 같은 간단한 수식(JSL Code)을 만들어야 합니다.
Log10(
Num( Substr( :Dilution, 3, 3 ) ) /
Num( Substr( :Dilution, 1, 1 ) )
)
Dilution 변수에서 3번째 자리수부터 3자리 값을 가져온 후 Log10값을 취합니다.
위와 같은 작업을 거친 후 X 축에는 Log(Dilution), Y축은 Percent Mortality값을 이용, JMP Graph Builder를 이용하여 곡선을 fitting시켜줍니다. 그 아래에는 전체 생존수/사망수에 대한 그래프도 함께 보여줍니다.
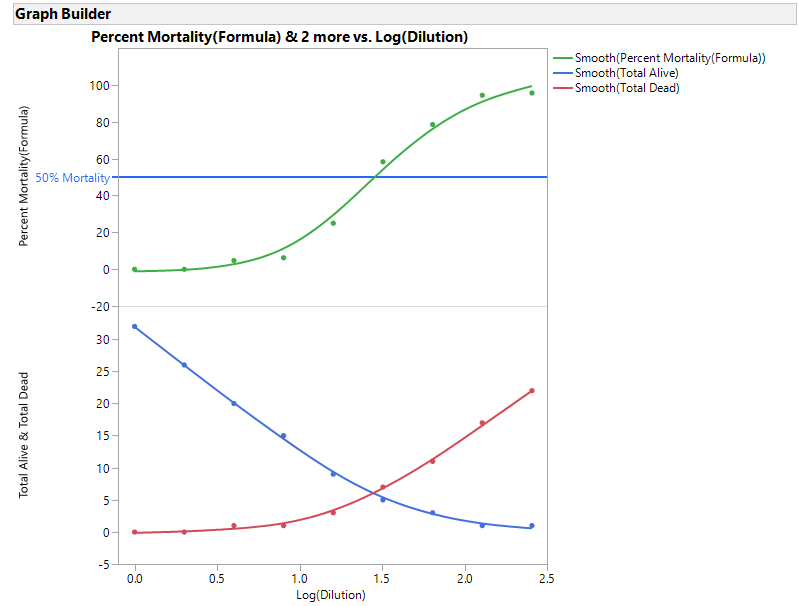
여기서 우리가 구하고자 하는 endpoint는 Percent Mortality값이 50%가 되는 Dilution입니다. 실제 논문에서는 보간법을 활용하여 수작업으로 계산하였으나, 여기서는 JMP의 Nonlinear Modeling 방법을 이용하여 그 값을 구해보도록 하겠습니다.
이 방법을 사용하기 위해선 Analyze >> Specialized Modeling >> Nonlinear 메뉴를 선택합니다.
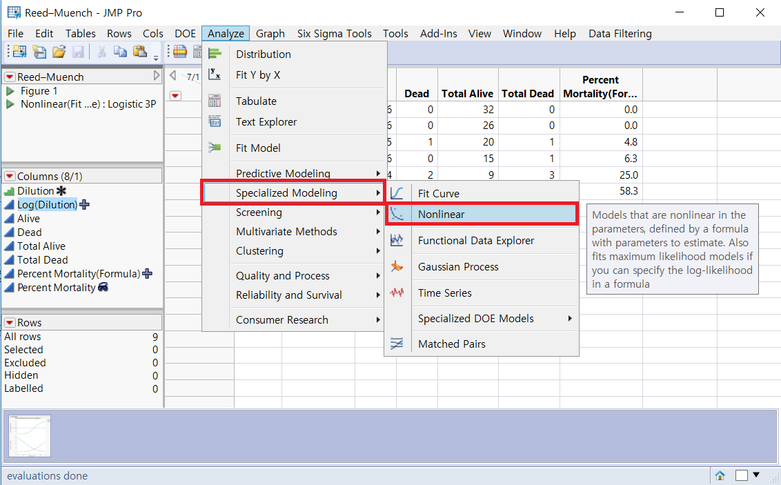
다음의 단계를 거칩니다.
1. Nonlinear Fitting(Logistic 혹은 Probit 혹은 Weibull 등)
2. 역추정을 통해 Percent Mortality가 50%가 되는 Log(Dilution)값을 추정
3. Log변환값을 되돌리기 위해 변환한다.
위 순서대로
1. Nonlinear Fitting
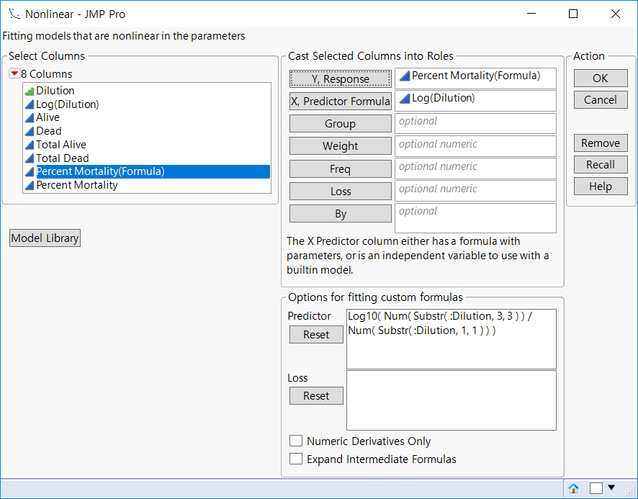
Y response 항목에는 Percent Mortality를 X Predictor Formula에는 Log(Dilution)을 지정합니다.
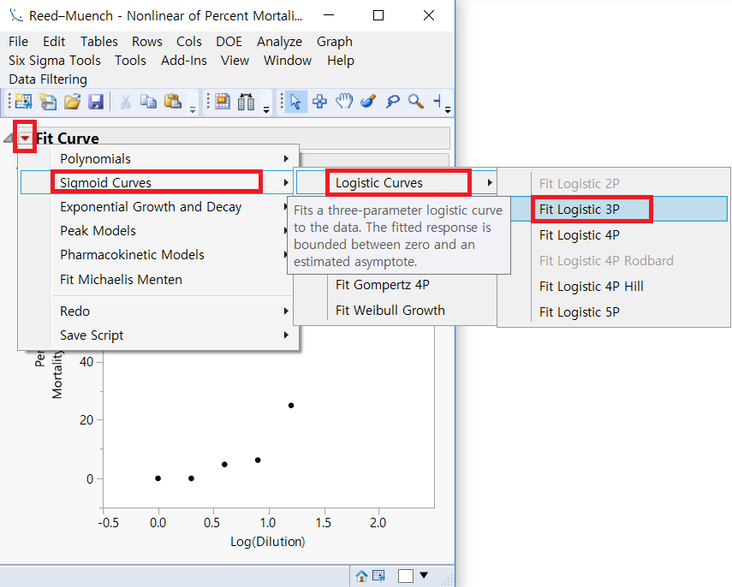
Fit Curve 좌측의 Hot Spot(Red Triangle)을 눌러서 Sigmoid Curve >> Logistic Curves >> Fit Logistic 3P를 선택합니다. 혹은 Probit이나 Weibull로 fitting 가능합니다.
2. 역추정을 통한 Percent Mortality 50%을 만족하는 Log(Dilution)값 추정
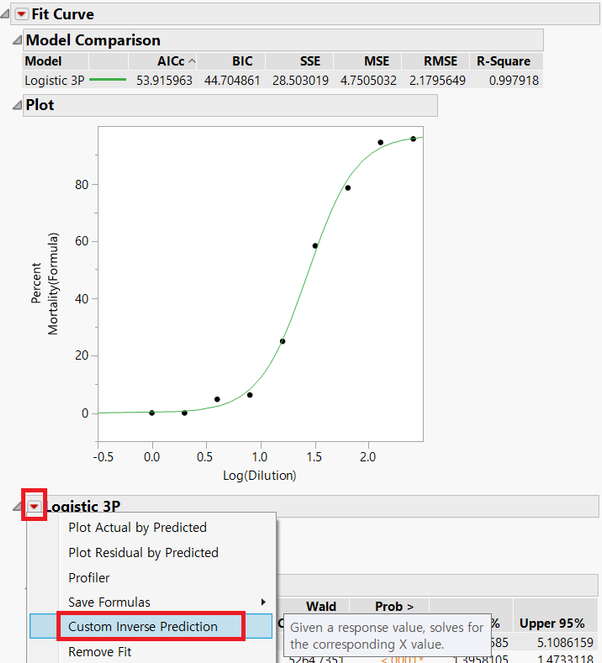
Logistic 3P 죄측의 Hot Spot 클릭 후 Custom Inverse Prediction 선택
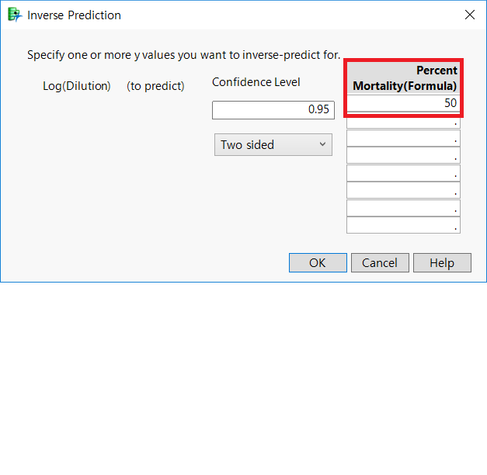
위 빨간 박스안에 원하는 값(50%)을 입력합니다.
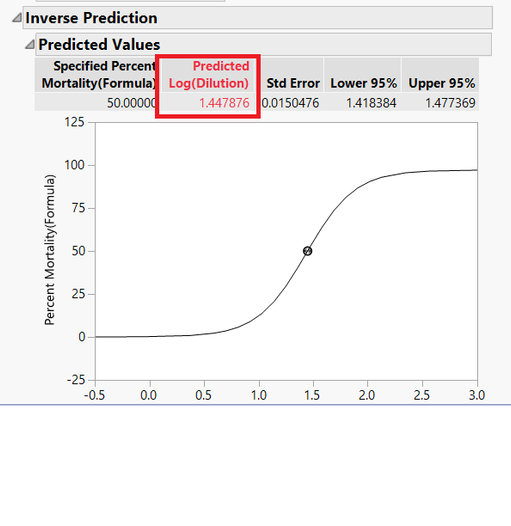
원하는 값인 1.447876을 구할 수 있습니다.
이를 이용해 다음 3단계인 변환을 위해 10^(1.447876)을 구하면 28.05를 구할 수 있습니다.
즉, 1:28이 Percent Mortality가 50%가 되는 Dilution endpoint가 됩니다.