JMP를 활용한 Biological Assays - 개념 및 PLA(Parallel Line Assay) 분석방법

[#1]

Biological Assay는 살아있는 세포 또는 조직에 미치는 효과에 의한 농도 또는 물질의 효능을 결정하는 분석방법을 의미합니다. 유럽 약전(European Pharmacopoeia)에서는 5.3항에 디자인/분석/타당성 검사등과 관련된 상세한 내용을 제공하고 있으며, 이는 미국 약전(USP 1032-1034) 및 ICH Q2R과도 동일한 내용입니다.

Bioassay 분석에서는 아래와 같은 여러 분석 디자인이 있으나, 본고에서는 PLA(Parallel Line Assays)에 한해 설명하도록 하겠습니다.

1. Parallel Line Model

2. Slope-Ratio Model

3. Quantal Responses

4. Extended Sigmoid Dose-Response Curves

먼저, Bioassays에 있어 실험결과 data는 다음과 같은 세가지 조건을 만족할 때 "통계적으로 타당하다(Statistically Valid)"라고 합니다.

1. 선형회귀 계수가 통계적으로 유의해야 합니다. 즉 선형회귀 계수의 p-value가 0.05보다 작아야 합니다.

2. 직선들간 평행성이 만족되어야 합니다. 즉 비평행성을 나타내는 항의 p-value가 0.05보다 커야 합니다.

3. 모든 직선은 선형성을 만족해야 합니다. 즉, 2차항 회귀계수의 p-value가 0.05보다 커야 합니다.

위와 같은 사전 개념을 먼저 학습한 후 EP 5.3에서 제공되는 example로 사례분석을 해 보겠습니다.

아래의 sample data는 "Two-Dose Multiple Assay with Completely Randomized Design" 사례입니다. 

위 데이터를 아래와 같이 JMP Data Table로 불러들입니다. 

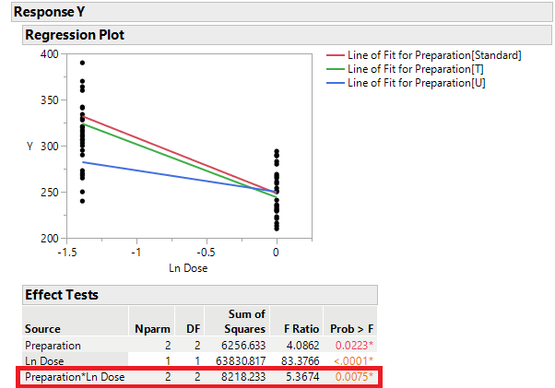
분석을 하기 전 아래와 같은 두개의 그림을 그립니다. 좌측의 그림은 세개의 Preparation 별로 Regression fitting 결과이며, 우측의 경우 세개의 Preparation을 Overlay한 plot입니다. 우측 그림을 봤을 때, Preparation U는 Standard와 T와는 평행성이 만족되기 힘들 수 있음을 알 수 있습니다.

  

  

분석은 먼저, 위에서 언급한 세가지 조건(회귀계수의 유의성 / 평행성 / 직선성)을 만족하는 지 살펴보고, 세가지 조건이 만족되었을 때 Relative Potency 를 구해보도록 하겠습니다.

1. 회귀계수의 유의성 : 각 Preparation 별 직선회귀 계수의 p-value가 0.05보다 작기 때문에 회귀계수의 유의성을 만족한다고 판단할 수 있습니다.

2. 평행성 : 세개의 직선에 대한 평행성에 관련된 항의 p-value는 0.05보다 작기 때문에 평행성을 만족한다고 볼 수 없습니다.

다만, Preparation U를 제외했을 때는 평행성을 만족한다고 할 수 있습니다.

  

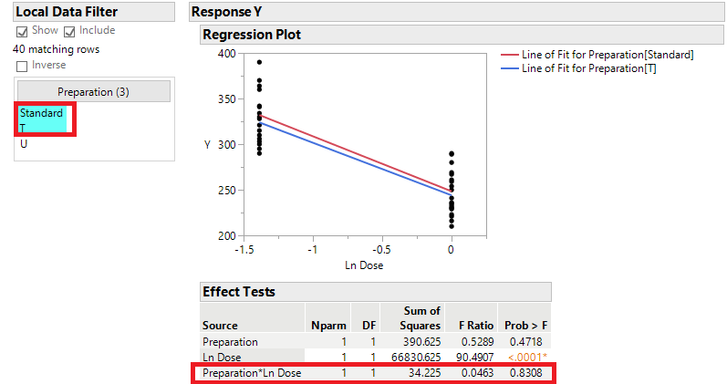
참고 : 위 결과는 다음과 같이 해석할 수 있습니다. 위에서 평행성을 나타내는 항(Term)은 실험계획법에서 2인자 교호작용을 나타내는 Term입니다. 즉 아래의 그림과 같이 2인자 교호작용(Interaction)이 존재한다는 것은 그 항이 통계적으로 유의하다(p-value가 0.05보다 작다)는 것을 의미하는 것입니다. 다시 말해, 위와 같이 해당 항이 통계적으로 유의하지 않다(p-value가 0.05보다 크다)는 것은 아래의 그림처럼 No Interaction으로 두 직선이 평행하다는 것으로 판단할 수 있습니다.

 

 

3. 선형성 : 본 사례에서는 Dose Level이 두가지로서 곡선을 Test해 볼 필요가 없습니다. 다만 Dose Level이 3개 이상인 경우 2차항을 fitting하여 1차항의 회귀계수와 2차항의 회귀계수가 각각 통계적으로 유의한지(p-value가 0.05보다 큰지 작은지)에 대해 검정함으로써 선형성을 확인할 수 있습니다.

[Relative Potency 구하는 방법]

아래와 같은 대화창에서 Red Triangle 클릭 후 Estimate >> Expanded Estimates를 클릭합니다.

아래와 같은 결과가 나오면  Standard 대비 Preparation T의 Relative Potency(물론 여기서는 자연로그기 씌워져 있는 상태입니다)는

(Preparation T의 기울기-Standard Preparation 기울기) ÷ 공통기울기

의 공식으로 구해집니다. 

 

 

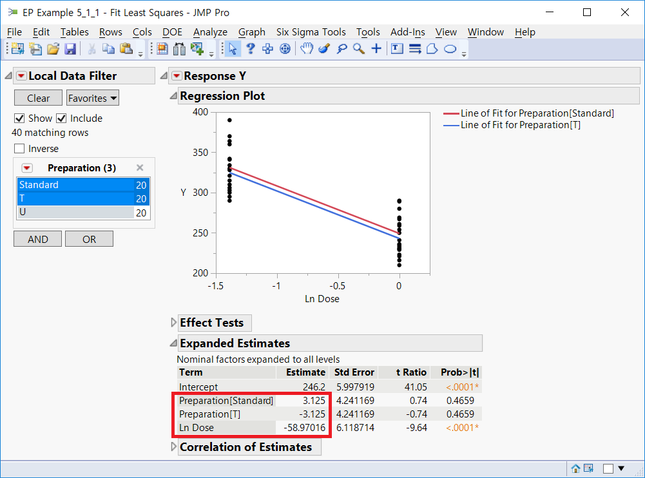
즉, (-3.125-3.125)/(-58.97016) = 0.1060이 Preparation T의 Relative Potency입니다.