See how to:
- Understand the difference between a Null and an Alternate Hypothesis, the two conditions that we want to investigate
- Null Hypothesis - generally the status quo, e.g. There is NO DIFFERENCE in the population means from which these two samples were drawn
- Alternative Hypothesis - the complement of the Null, e.g. There IS A DIFFERENCE in the population means
- We can also insert Greater Than (or Less Than) instead of No Difference
- Accepting Alternate Hypothesis is rejecting (or disproving) Null Hypothesis
- When running tests, we look for proof that the Alternative Hypothesis is within our confidence level, and we can Refute (or Disprove) the Null Hypothesis
- Caution: If we DO NOT reject the Alt, it DOES NOT mean that the Null is true and perhaps we didn't collect enough data to accept it.
- Confidence Level is the level of surety involved with the hypotheses
- Confidence Level needed can depend
- Often, acceptable Confidence Level for making decisions is 95%.
- Perhaps if you are looking at life-or-death decisions, you need to be 99.9% confident in the results
- 95% confidence means if you run statistical test 100 times, your should be right about 95 times
- Alpha value is 1 - Confidence/100
- Compare and interpret Confidence Interval on a Mean Value
- Compare Mean to a Target Value
- Analyze>Distribution and then Test Mean from red triangle
- Interpret Quanitles, Summary Statistics, Means Test
- Compare two Means
- Analyze>Distribution and then t-test from red triangle
- Interpret t-test
- Compare more than Two Means
- Analyze>Distribution and then Means/ANOVA from red triangle
- Run Oneway analysis (ANOVA)
- Interpret Summary of Fit, R-square, Analysis of Variance and Means for one ANOVA
- Hypothesis Testing for Equivalence – Used because when sample means are not different, we still can’t conclude that the population means were the same
- Alternate Hypothesis is that Population Means are the same, within some specified margin
- Null Hypothesis is that the Population Means MAY NOT BE the same within the margin.
- Difference in Population Mean is outside the equivalence interval
- Employ 2-sided t-tests (TOST)
Note: Q&A is interspersed beginning at ~ Time 20:05.
If you have questions for Jerry, type @JerryFish in your comment.
Resources
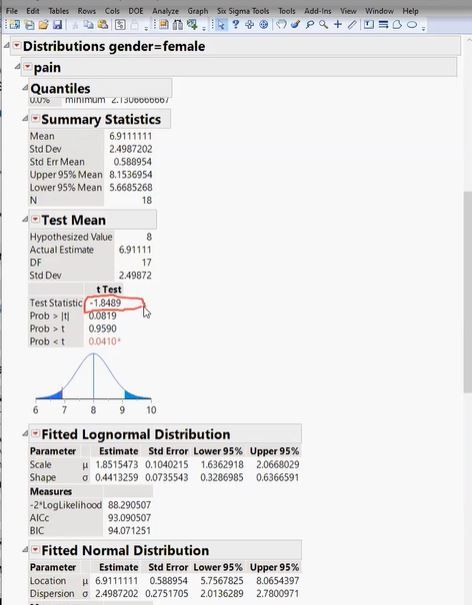 Compare Mean to Target ValueCompare Mean to Target Value
Compare Mean to Target ValueCompare Mean to Target Value