This technical presentation was given by Elizabeth Claassen, JMP Statistical Developer and co-author of JMP for Mixed Models for JMP. Data from the book was used in the presentation and is available for you to download and use. The video is over 90 mins. long with questions interspersed throughout.
Mixed models are one of the most powerful ways to handle correlated observations in designed experiments. They often go by other names, including blocking models, variance component models, nested and split-plot designs, hierarchical linear models, multilevel models, empirical Bayes, repeated measures, covariance structure models and random coefficient models.
Reaching well beyond standard linear models, mixed models enable you to make accurate and precise inferences about your data and to gain deeper understanding of sources of signal and noise in the system under study. Well-formed fixed and random effects generalize well and help you make the best data-driven decisions.
- Learn rationale and techniques behind JMP’s mixed model capabilities, see when and how to use mixed models, learn how to recognize, set up, and interpret fixed and random effects and see how to extend Analysis of Variance (ANOVA) and linear regression to numerous mixed model designs.
- See how to understand and use degrees of freedom: analyze randomized block, split-plot designs and random coefficient models; and address modern dilemmas around Bayesian methods and p-values.
- Definitions
- Fixed Effects are exact factors/levels and you want to make inference for a future observation from exactly those levels
- Random Effects are when the levels are a sample from a larger population, and you want to make inference to the larger population and not just to those specific levels, and/or when you are primarily interested in explaining the variability coming from that effect rather than, say, pairwise comparisons
- Mixed Models incorporate Random and Fixed Effects
- Mixed Models are useful for handling Random Effects and with a mixed model, we could have possibly different results for the estimates the confidence intervals and those pairwise comparisons compared to a fixed effect only model.
- LSMeans are not necessarily the arithmetic means. Missing data/imbalance needs REML to better estimate the LSMeans
- With missing data/ imbalance, the pairwise comparisons for the other fixed effects are also affected by the choice to model an effect as random.
- Don’t rely only on the p-value – remember that p=0.049 and p=0.050 are basically the same thing.
Q&A is included throughout. Some questions that came up were:
- What does the Wald p-value imply in that Bond data ANOVA table The Wald test statistic is being used to calculate the p-value (as opposed to, say, the F statistic). We show Wald test statistic but typically do not use it to evaluate the
- For this block example. Aren't you describing a nested situation? This behavior would happen in nested models, but this is not a nested example since treatment is not unique to block.
-
Can you give an example of such a 'badly' incomplete block designs, where do they appear in practice? This might happen when you have large fallout in a block because of attrition or processing that results in missing values. For example, when you have many different types of processing equipment and something goes awry causing missing values for one piece of equipment, places where you have imbalance, or for studies of people where you sample from different groups and different levels of attrition for some than for others. Another example is a taste test where some people taste some things and others taste others.
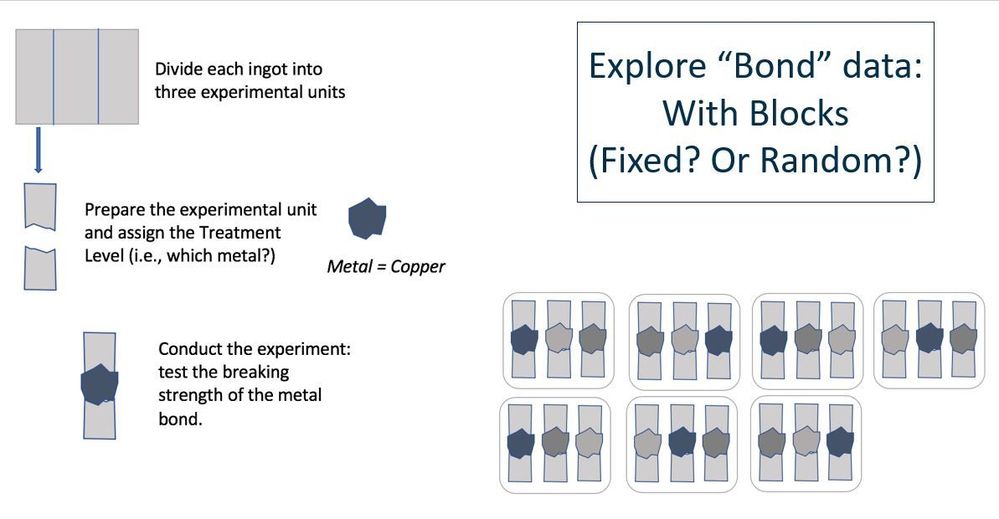 Learn how to determine Fixed and Random blocks/effectsLearn how to determine Fixed and Random blocks/effects
Learn how to determine Fixed and Random blocks/effectsLearn how to determine Fixed and Random blocks/effects
Resources: