- JMP User Community
- :
- Learn JMP
- :
- Mastering JMP
- :
- Deploying Stepwise Regression Methods in JMP and JMP Pro
The content you are looking for has been archived. View related content below.
Practice JMP using these webinar videos and resources. We hold live Mastering JMP Zoom webinars with Q&A most Fridays at 2 pm US Eastern Time. See the list and register. Local-language live Zoom webinars occur in the UK, Western Europe and Asia. See your country jmp.com/mastering site.
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
See how to use JMP and JMP Pro to identify important predictors suitable to predictive modeling, reducing variance caused by estimating unnecessary terms, and building predictive models. See case studies that show how to use JMP Stepwise Regression to find important variables and active model effects and how that approach compares to JMP Pro Generalized Regression techniques that automatically incorporate variable selection.
See how to:
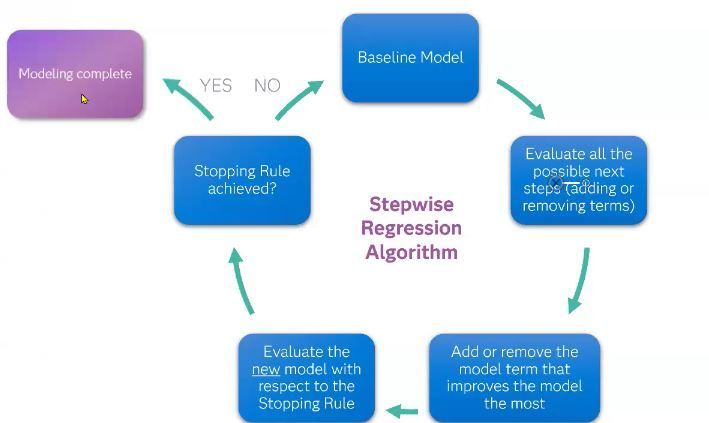
- Understand the underpinnings of the stepwise regression method
- Choose stepwise regression options to automate factor selection
- Analyze > Fit Model > Personality: Stepwise
- Set stopping rule/criteria
- Set forward, backward or mixed direction
- Forward selection selects the variable with the lowest p-value, adds it to the model, and then recalculates the p-values, and stopping criteria until stopping criteria are satisfied
- Backward elimination selects the variable with the highest p-value, removes it from the model, and then recalculates the p-values and stopping criteria until stopping criteria are satisfied
- Mixed alternates between forward selection and backward elimination, using p-value as stopping criteria
- Run the model
- Use additional stepwise options
- Alternate stopping rule - KFold validation R2
- Build and compare all possible models
- Use model averaging based on the AICc weight in each model
- Implement stepwise methods in JMP Pro Generalized Regression to easily deploy variable selection, validation, penalized regression to help with correlated factors, interactive model visualization, compare models, relaunch models easily with higher order terms
- Understand the advantages and limitations of Stepwise and Generalized Regression approaches
Questions answered by Scott Allen @scott_allen and Byron Wingerd @Byron_JMP at the live webinar:
Q: Is there a guideline for when AICc is preferred over BIC?
A: BIC gives you the best model with the fewest terms; AICc gives you the model that explains the most variation and it is penalized by the number of terms. The lower case c in AICc stands for corrected and it means corrected for small data sets. The AIC tries to select the model that most adequately describes an unknown, high dimensional reality. This means that reality is never in the set of candidate models that are being considered. On the contrary, BIC tries to find the TRUE model among the set of candidates.
The short answer is, I just run them both and compare them or you could even take the 2 and then average them together. You have the tools here in the Stepwise platform to carry out those and then compare them and automatically compare the results in a graph. In some cases. it depends on your goal, if you are OK having more terms or are you really looking to reduce this to the minimum set. In the example with 500 data points, BIC is probably preferred.
Q: How do we check over fitting?
A: If we're just fitting linear models in JMP, even using Stepwise, it will be little bit more tricky to identify overfitting issues. In JMP Pro, we can set up test, training and validate subsets (or if you prefer, at least test and training) and compare the R-squares. So, if you see that the training set has really great R-squared and your validation has a really terrible R-squared, it means you fit the data well and you're not going to be very predictive of future observations.
Q: In the model, a total of 568 row also have validation rows. re we using all those in model or are we keeping them?
A: They are being held out for validation and evaluated separately as the validation subset.
Q: In the old SAS Enterprise Miner, the "Ensemble" node often performed best. What do you think about running a bunch of models, saving the predictions, and then simply averaging all those predicted values?
A: In JMP, we use the neural net platform to set up an ensemble model. They generally tend to out perform the individual models.
Q: How did you get the color map for correlations?
A: Under the red triangle, look for the color map options.
Q: How do you detect and handle multicollinearity?
A: Stepwise alone in JMP is not going to handle the multicollinearity so you’d have to pull them out ahead of time and/or find a representative variable using clustering. If you are in JMP Pro Generalized Regression, penalized regression methods will help address that as well so, if you are really concerned about it, generalized regression is definitely the way to go. You could build that least squares model, run it and look at your parameter estimates. High VIF values might indicate multicollinearity. See video below.
Resources
- Video and Q&A on Specifying and Fitting Models
- Free STIPS module on Crrelation and Regression
- Learning about multicollinearity
- How to use JMP to detect and handle multicollinearity when building models
Thanks for the webinar! And this thanks extends to Scott Allen as well.
It was a great learning and I was eager to apply the new learning right away to my data.
When I applied the newly learnt K-folder regression method, I got mixed results.
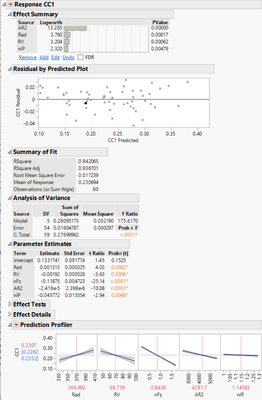
- Original Regression analysis by Stepwise prior to this webinar session: With a default setting on Rule, Direction and others, I ran it for a model which is listed below first (Pic1). I did further narrow the model down by removing term(s) of p-value >0.05 and more simplifications (reduction terms within a reasonable adj-R2 values). I was happy with that results.
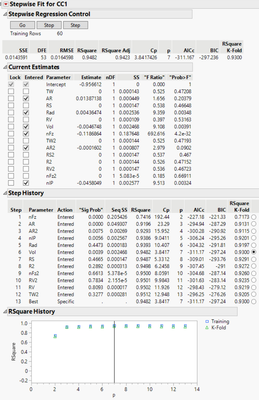
- Later analysis by the same Stepwise after this webinar: By changing the rule to ‘Max K-fold RSquare’, I repeated the analysis to get the preliminary Analysis (Pic2). Although the preliminary results shows Max R values with 13 terms as the best. I don’t want that many terms in my model and I was OK with R-value level with 5~6 terms for both Training & K-Fold. So, I chose the results of 6-terms as seen and ran the model.
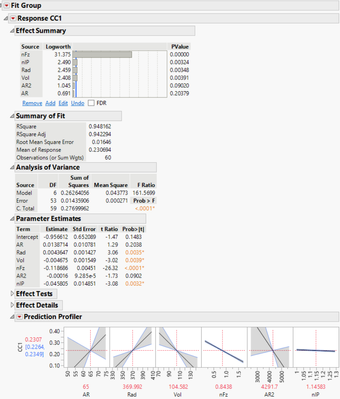
As you can see, its model includes a term of PValue >0.05 in Pic3. Also, in its profile, the confidence/variance level is very wide for most terms. So I removed AR term to have a similar R-values and similar model to my original model – except ‘RV’ of the original model was replaced with ‘Vol’ term in the new model. These 2 terms of RV & Vol could carry similar information but not exactly same. I don't know why K-fold rule like one over the other term.
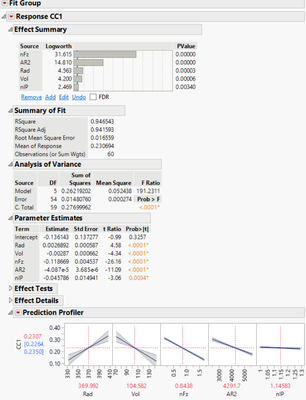
Anyway, I am happy with the results since they came in a similar way of modeling which confirms that my original model was not too bad (without separate training & validation process. That is how I understood about K-fold method dividing the data set into 2 groups of subset to use one group for training and the other for validation. Am I right?)
Here is my 2nd question if the above is counted as the 1st question:
Although K-Fold method resulted in a slightly better by yielding R2 of 0.947, I still prefer the original results R2 of 0.942. That is because its model carries a less uncertainties in modeling profiler for the terms of Rad & RV comparing to the new results by K-Fold. K-Fold method can be simply used for this kind of model validation or more if the original approach was not good enough.
For this specific example, it was not a difficult decision since R2 values were not largely different.
But, if R2 values are low by 0.1 (with 2-3 less terms) in the original model, but it has much less variance in prediction profiler (like the original model vs. model in Pic3), which model would be better?
I am currently using JMP 17.
Pic1: Original Analysis
Pic2: Preliminary Regression by K-fold Rule
Pic3: Model by K-Fold
Pic4: Final Results by K-Fold Method
Hi @SeanL
In Pic3, the confidence intervals that look like "bowties" in your Profiler are a good indicator that you have some highly correlated variables. Since stepwise regression checks the effect of each variable on the model independently, it will not always detect correlated variables.
To verify this, you can check the VIFs by right clicking the table in the Parameter Estimates table and adding the VIF column. Any VIF value >10 indicates that collinearity is likely an issue. The Statistics Knowledge Portal has a good overview here.
It seems like this is resolved in Pic 4 when you remove one of the variables manually.
You can run Multivariate analysis on all of your variables to check for correlation and then choose the most representative variable for your modeling. You can also watch the Mastering JMP webinar on Building Predictive Models for Correlated and High Dimensional Data.
Regarding ensemble models, @scott_allen wrote: There are other ways to build ensemble models in Standard JMP and JMP Pro. You can simply average models together in Standard JMP manually (sum them up and divide by numthe ber of models). In JMP Pro you can ensemble different models using the Compare Models platform. Also, see 2021 Ensemble Model presentation by @Peter_Hersh .
Recommended Articles
- © 2024 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- About JMP
- JMP Software
- JMP User Community
- Contact