Deploying Stepwise Regression Methods in JMP and JMP Pro

See how to use JMP and JMP Pro to identify important predictors suitable to predictive modeling, reducing variance caused by estimating unnecessary terms, and building predictive models. See case studies that show how to use JMP Stepwise Regression to find important variables and active model effects and how that approach compares to JMP Pro Generalized Regression techniques that automatically incorporate variable selection.

See how to:

• Understand the underpinnings of the stepwise regression method
• Choose stepwise regression options to automate factor selection
  • Analyze > Fit Model > Personality: Stepwise
  • Set stopping rule/criteria
  • Set forward, backward or mixed direction
    • Forward selection selects the variable with the lowest p-value, adds it to the model, and then recalculates the p-values, and stopping criteria until stopping criteria are satisfied
    • Backward elimination selects the variable with the highest p-value, removes it from the model, and then recalculates the p-values and stopping criteria until stopping criteria are satisfied
    • Mixed alternates between forward selection and backward elimination, using p-value as stopping criteria
  • Run the model
• Use additional stepwise options
  • Alternate stopping rule - KFold validation R2
  • Build and compare all possible models
  • Use model averaging based on the AICc weight in each model
• Implement  stepwise methods in JMP Pro Generalized Regression  to easily deploy variable selection, validation, penalized regression to help with correlated factors, interactive model visualization, compare models, relaunch models easily with higher order terms

• Understand the advantages and limitations of Stepwise and Generalized Regression approaches

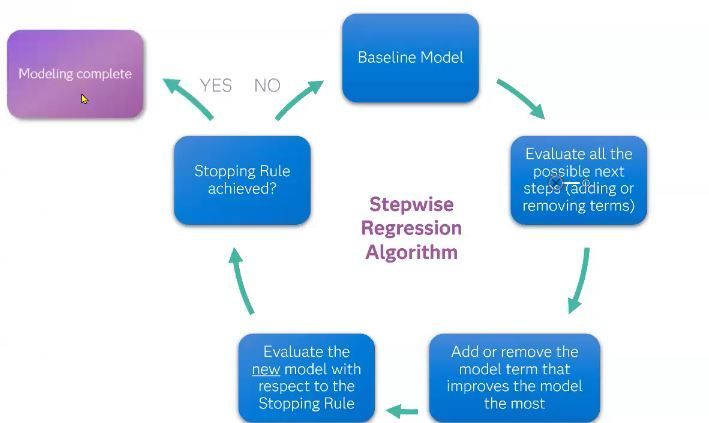JMP Stepwise Regression FlowJMP Stepwise Regression Flow

Questions answered by Scott Allen @scott_allen and Byron Wingerd @Byron_JMP at the live webinar:

Q: Is there a guideline for when AICc is preferred over BIC?

A: BIC gives you the best model with the fewest terms;  AICc gives you the model that explains the most variation and  it is penalized by the number of terms. The lower case c in AICc stands for corrected and it means corrected for small data sets. The AIC tries to select the model that most adequately describes an unknown, high dimensional reality. This means that reality is never in the set of candidate models that are being considered. On the contrary, BIC tries to find the TRUE model among the set of candidates.

The short answer is, I just run them both and compare them or you could even take the 2 and then average them together. You have the tools here in the Stepwise platform to carry out those and then compare them and automatically compare the results in a graph.  In some cases. it depends on your goal, if you are OK having more terms or are you really looking to reduce this to the minimum set. In the example with  500 data points, BIC is probably preferred.

Q: How do we check over fitting?

A: If we're just fitting linear models in JMP, even using Stepwise, it will be little bit more tricky to identify overfitting issues. In JMP Pro, we can set up test, training and validate subsets (or if you prefer, at least test and training)  and compare the R-squares. So, if you see that the training set has really great R-squared and your validation has a really terrible R-squared, it means you fit the data well and you're not going to be very predictive of future observations.

Q: In the model, a total of 568 row also have validation rows. re we using all those in model or are we keeping them?

A: They are being held out for validation and evaluated separately as the validation subset.

Q: In the old SAS Enterprise Miner, the "Ensemble" node often performed best.  What do you think about running a bunch of models, saving the predictions, and then simply averaging all those predicted values?

A: In JMP, we use the neural net platform to set up an ensemble model. They generally tend to out perform the individual models.

Q: How did you get the color map for correlations?

A: Under the red triangle, look for the color map options.

Q: How do you detect and handle multicollinearity?

A: Stepwise alone in JMP is not going to handle the multicollinearity so you’d have to pull them out ahead of time and/or find a representative variable using clustering. If you are in JMP Pro Generalized Regression, penalized regression methods will help address that as well so, if you are really concerned about it,  generalized regression is definitely the way to go.  You could build that least squares model, run it and look at your parameter estimates. High VIF values might indicate multicollinearity. See video below.

Resources

• Video and Q&A on Specifying and Fitting Models
• Free STIPS module on Crrelation and Regression
• Learning about multicollinearity
• How to use JMP to detect and handle multicollinearity when building models