뉴스레터 구독자에게 발송되는 Monthly User Guide입니다. 관련 문의는 ikju.shin@jmp.com으로 부탁드립니다.
많이 알려진 대로, ANOVA(분산 분석, Analysis of Variance)는 연속형 반응치(Continuous Response)에 대한 범주형 인자(categorical factor)의 유의성, 영향도를 평가하는 가장 대표적인 방법입니다. ANOVA 의 종류에는 일원 분산 분석(OneWay ANOVA), 이원 분산 분석(Two-Way ANOVA) 등이 있는 데, 이 때 일원 또는 이원의 의미는 요인의 개수를 말합니다. 예를 들어 재료 A, B 의 따른 수율의 차이를 검정한다면 요인은 재료 하나 이므로 일원 분산 분석이고, 반면 재료 A, B 및 가열 온도 100 도, 110 도에서의 수율의 차이를 검정하고자 한다면 요인은 재료 및 온도 두 가지이므로 이런 경우를 이원 분산 분석이라고 합니다. 재료 A, B 또는 온도 10 도, 110 도처럼 각 요인의 수준(Level)이 두 가지일 경우가 ANOVA 의 가장 기본적인 형태라 볼 수 있는 데, 여기서는 요인의 수준(Level)이 세 가지 이상인 경우인 다중 비교(Multiple Comparison)에 대해 살펴보겠습니다.
일반적으로 ANOVA(Analysis of Variance, 분산 분석)를 사용하여 평균치 차이 검정을 할 경우 가설은 다음과 같습니다.
1) 귀무 가설(Ho) : 모든 그룹의 평균은 같다.
2) 대립 가설(H1) : 모든 그룹의 평균이 같은 것은 아니다.
핵심은 적어도 한 그룹의 평균이 다른 그룹의 평균과 다르면 귀무 가설을 기각하는 데에 있습니다. 즉 귀무 가설을 기각한다고 해서 모든 그룹의 평균치 차이가 나는 것이 아니라는 점입니다. 이와 같이 다중 비교(Multiple Comparison)의 경우 어떤 문제가 생길 수 있는 알아보겠습니다.
예를 들어 A, B, C, D, E 다섯 Group 을 가진 X 인자를 가지고 ANOVA 방법을 활용하여 두 Group 간 평균치 차이 검정을 한다고 가정하면 모두 10 가지의 비교가 가능합니다. 이 때 유의 수준(α, 1 종 오류) 0.05 기준으로 Test 전체의 위험률은 0.401 이 됩니다. 왜냐하면 유의 수준(1 종 오류)이 0.05 일 때, 1 종 오류가 발생하지 않을 확률은 (1-0.05) = 0.95 가 되는 데, 10 가지의 비교에 대해 1 종 오류가 발생하지 않을 확률은 (0.95)10 = 0.599 가 됩니다.
즉, 10 가지의 비교에서 적어도 하나의 비교에서 1 종 오류가 발생할 확률은 1 – 0.599 = 0.401 이 되어 유의하지 않는 데도, 유의한 차이가 있다고 해석할 가능성이 높아지게 되므로, 다중 비교의 경우에는 일반적인 ANOVA 의 경우와는 좀 다른 방법과 해석이 필요합니다.
JMP 내의 아래 Sample Data 를 가지고 살펴보겠습니다.
(Help / Sample Data Library / big class.jmp)
나이에 따라 키의 평균의 차이가 나는 지를 확인하기 위해 Analyze / Fit Y by X 에서 age 를 X 로, height 를 Y 로 선택하여 OK 클릭합니다. ▼Oneway ~ / Means / Anova 를 실행하면 결과는 아래와 같습니다.
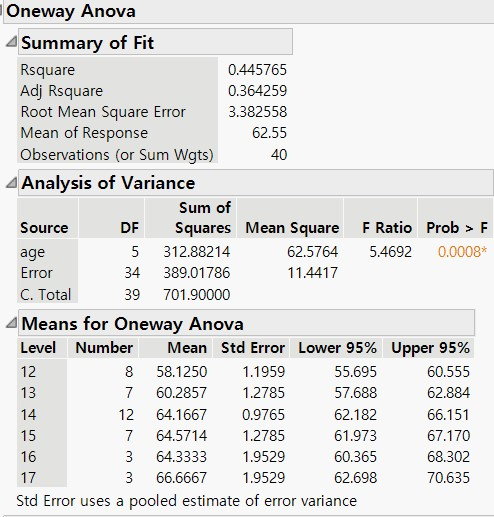
위의 결과에서 P Value(0.0008) 만을 보고 나이에 따라 키 차이가 난다고 판단하면 안됩니다. 여기서는 여섯 가지 나이 Level(12 살 ~ 17 살) 중 적어도 하나 이상의 Level 간에 차이가 난다는 뜻이지 모든 나이 Level 간에 차이가 난다는 뜻이 아니므로 조심해야 합니다.
이와 같이 3 개 이상의 다중 비교일 경우에는 ▼Oneway ~ / Compare Means 아래에 있는 다섯 가지 방법 중 어느 하나를 사용해야 합니다. 여기서는 다섯 가지 방법 모두를 실행해 보겠습니다. (alt Key 를 누른 상태에서 Oneway 옆의 붉은 색 삼각형을 클릭하면 다섯 가지 방법 모두를 한꺼번에 실행할 수 있습니다.)
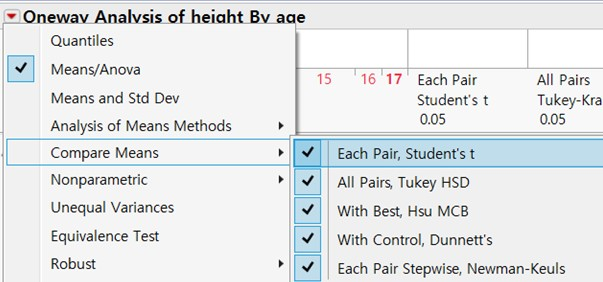
다섯 가지 방법에 대해 간략히 정리하면 아래와 같습니다.
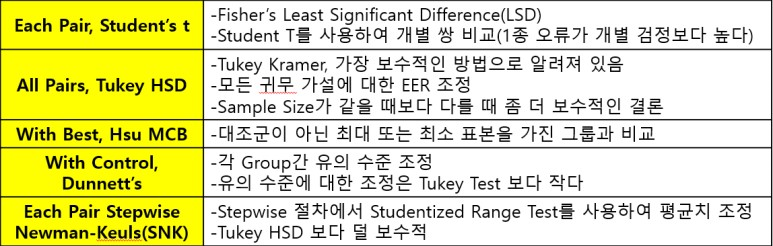
1. Each Pairs, Student's t
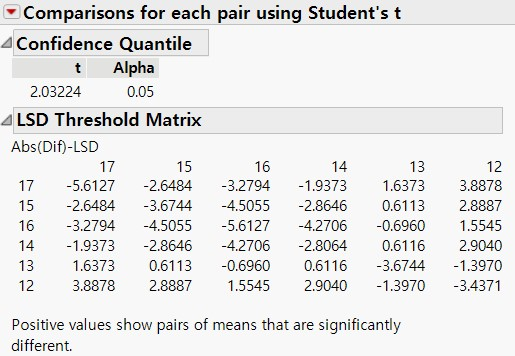
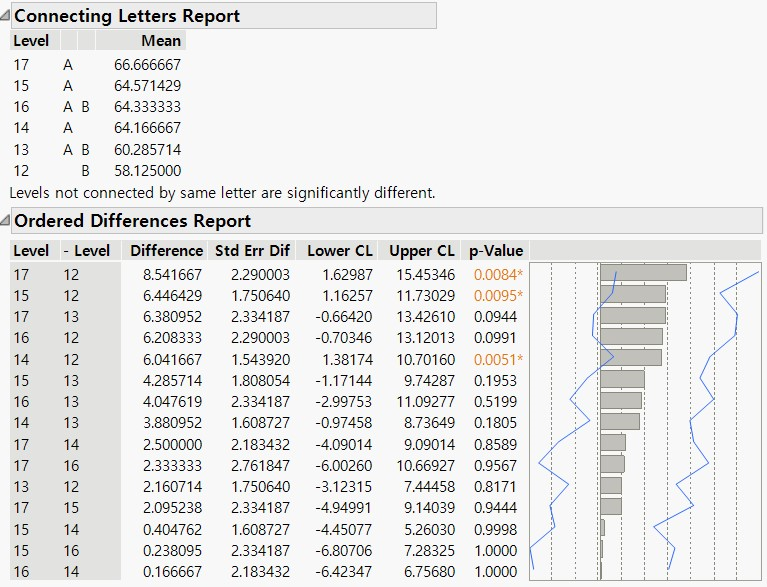
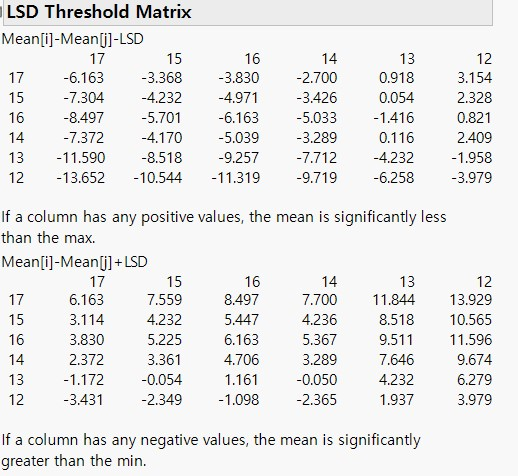
1) LSD Threshold Matrix 에서는 양수 값으로 포현된 Level 끼리는 유의한 차이가 있다는 뜻입니다.
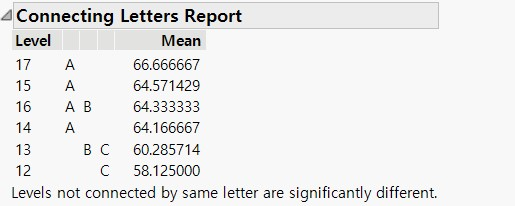
2) Connecting Letters Report 에서는 같은 문자가 포함된 Level 은 유의한 차이가 없다는 뜻이 됩니다.
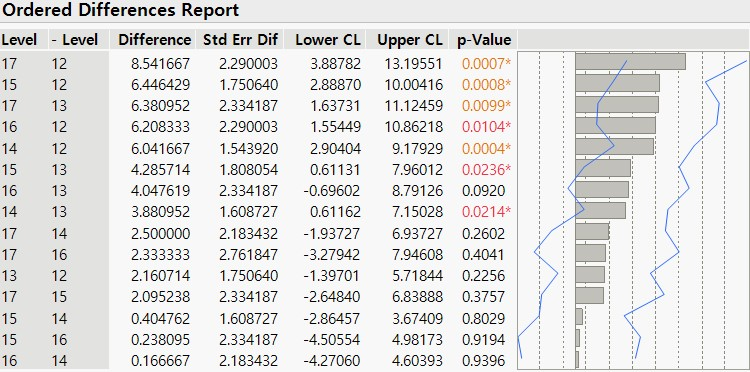
3) Ordered Difference Report 에서는 두 Level 간 검정 결과가 요약되어 있습니다.
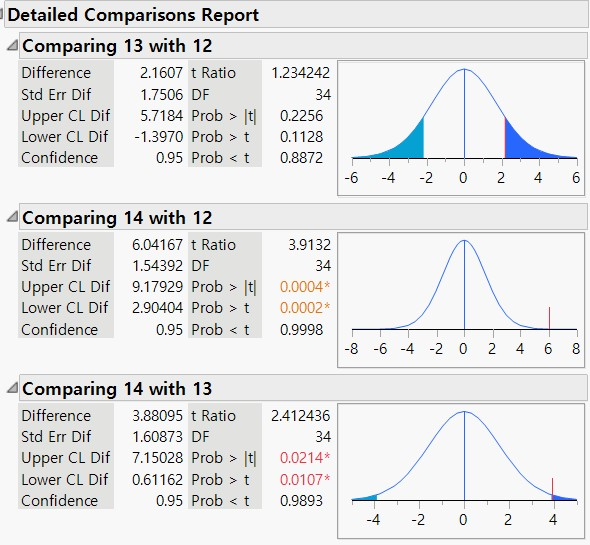
4) ▼Comparisons / Detailed Comparison Report 를 클릭하면 아래와 같이 두 Level 간 비교 결과(여기서는 비교 대상 Level 이 6 가지 이므로 모두 15 가지의 비교 결과)를 모두 확인할 수 있습니다.
2. All Pairs, Tukey HSD(Honestly Significant Difference)
위의 Student's t 검정 대비 결과가 상당히 보수적입니다. (통계적 유의성을 매우 엄격하게 해석하므로 이러한 해석이 필요한 상황에서 실무적으로 많이 활용됩니다.)
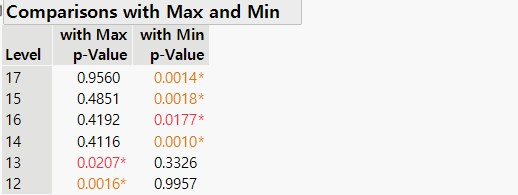
3. With Best, HSu MCB
이 방법은 최소 또는 최대 Sample Size 를 가진 Group 과 비교하므로 위의 두 방법과는 다소 다른 검정 결과를 보여줍니다.
4. With Control, Dunnett's
이 방법은 하나의 비교 그룹(여기서는 12 살을 비교 그룹으로 선택) 기준으로 검정하는 방법입니다.

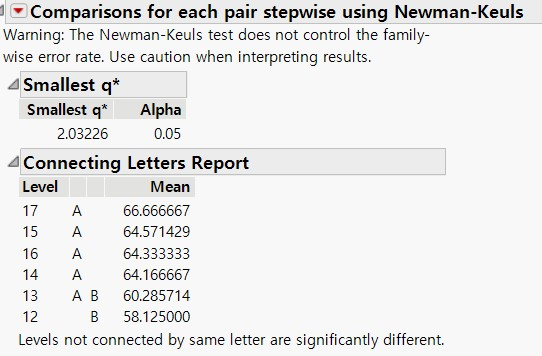
5. Each Pair Stepwise Newman Keuls(SNK) 의 결과는 아래와 같습니다.
6. 종합적 해석
1) 실무적으로는 Student's T 방법과 Tukey-Kramer(Tukey HSD) 방법을 가장 많이 활용하는 것 같습니다.
2) 이 중에서도 Tukey-Kramer 방법이 보다 보수적이고 엄격합니다.
3) 상단에 있는 Circle 중의 어느 하나를 클릭하면 아래와 같이 유의차가 없는 Level 은 같은 붉은 색으로, 유의차가 있는 Level 은 검은 색으로 표시됩니다. 아래는 TurkeyKramer 방법의 13 살을 선택했을 때의 결과입니다. (마지막 방법인 Stepwise Newman Keuls(SNK)은 이러한 Circle 이 표시되지 않습니다.)