Using Loc with a 2D Matrix

2 Kudos

Problem

You have a 2D matrix. You used the Loc function to locate interesting elements, but Loc returned indexes for a 1D matrix. How can you convert the 1D indexes back to 2D indexes?

Solution

You'll need to use the Floor and Mod functions and you'll need to know the number of columns in your 2D matrix. Here's the three lines, buried in the commented example below. pixmat is a 2D matrix, Loc is finding the non-zero pixels, which are black:

blacklocs = (Loc( pixmat ) - 1); // blacklocs is a matrix of 1D indexes (0-based)

rowlocs = Floor( (blacklocs) / nc ) + 1; // nc is the number of columns in the 2D pixmat
collocs = Mod( (blacklocs), nc ) + 1; // rowlocs and collocs are 2D indexes (1-based)

// we need a bitmap to work with; use a text box with a moderate size font
textbox = Text Box( "Gargoyle", <<setfontsize( 20 ) );
// get a picture from the text box
picture = textbox << getpicture;
// get the red pixels in a matrix. green or blue 
// would work as well, it is shades of gray.
pixmat = picture << getpixels("r"); // {[ red matrix]}
// the list would have more elements if you asked for "rgb".
// go ahead and pull out the only element.
pixmat = pixmat[1]; // [red matrix]
// the matrix of pixels is 0 for black, 1 for white, and .5 for a middle gray
// the values > .5 are antialiasing fading to white background of the "paper". 
// the next statement makes the 0 to .5 values be 1 and the .5 to 1 values be 0
pixmat = pixmat < .75; // cut off edge at some gray value. flip the 0..1 significance.
// the pixels are in a 2D matrix of rows and cols. get the dimensions.
nr = N Rows( pixmat );
nc = N Cols( pixmat );
// now we can find the location of the black pixels (1s) that form the text.
// the LOC function returns a 1D matrix of the offsets of non-zero
// elements in the 2D matrix pixmat. if pixmat was 3 rows of 5 elements each,
// the LOC could return a 1D matrix of 0 to 15 elements with values from 1 to 15.
// JMP uses 1-based indexing. subtract one to get 0-based for future steps.
blacklocs = (Loc( pixmat ) - 1);
// Here's the JSL that convers the 1D answers back to 2D answers.
// use the 0-based blacklocs (previous statement), then add 1 to 
// turn the 0-based results back into the 1-based indexes JMP expects.
rowlocs = Floor( (blacklocs) / nc ) + 1;
collocs = Mod( (blacklocs), nc ) + 1;
// Show the results
scale = 16; // try bigger or smaller scale for your screen size
New Window( "Example",
    Graph Box(
        // make the graph the same aspect ratio as the bitmap
        framesize( nc * scale, nr * scale ), 
        // make the point marker size big; .65 is approximately right
        <<Marker Size( scale * .65 ), 
        // the x axis is the columns in the matrix
        xaxis( {Min( -1 ), Max( nc + 1 )} ), 
        // the y axis needs to flip the rows in the matrix
        yaxis( {Min( nr + 1 ), Max( -1 )} ), 
        // Marker takes a pair of matrices, one for the x, and one for they,
        // are draws a marker at each x-y position. The columns are x
        // and the rows are y. the yaxis, above, put row 1 at the top.
        Marker( collocs, rowlocs ) // <<<< here are the 2D coordinates <<<<
    )
);

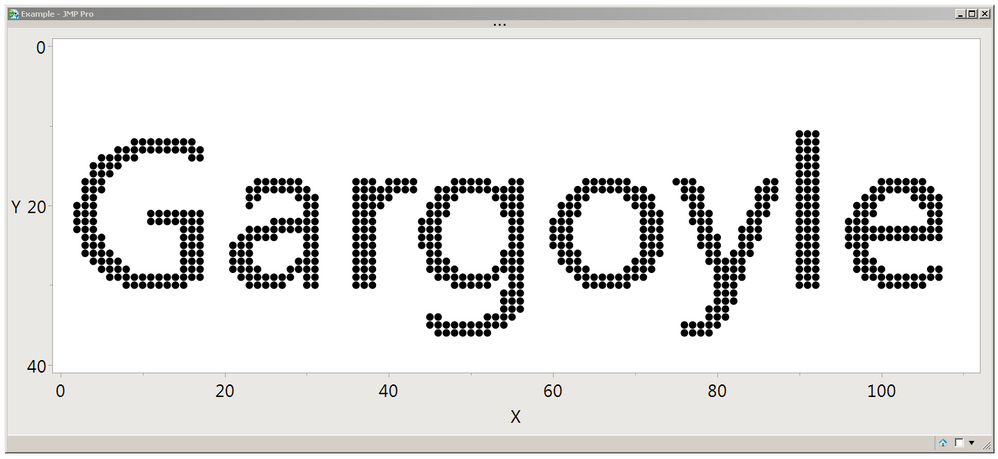Pixels from a bitmap, displayed as markers in a graph

Discussion

The -1 and +1 are important, don't leave them out. Read the 1-based and 0-based comments in the JSL.

The text in the bitmap is anti-aliased, which means the edge pixels are shades of gray proportional to how the perfect edge of the character would have fallen between pixels. I chose a gray threshold of .75 because I liked the result better than .5; your application probably won't be dealing with that at all.

JMP's Shape() function converts the shape of a matrix. That won't help here.

Many of the statements in the example are operating on a matrix without using an explicit JSL for-loop. Good for speed.

Problem

Solution

Discussion

See Also