Population structure is genetic similarity across large groups of individuals or lines. In preparation for association mapping, population structure should be assessed. Like familial relatedness, population structure can be incorporated into an association mapping analysis. In QK association analysis, population structure is modeled with a Q matrix, and familial relatedness is modeled with a K matrix (See Part 3a: Marker Based Relationship Matrix). There are two ways to construct a Q matrix in JMP Genomics: Principal Components Analysis (PCA) and Multidimensional Scaling (MDS).
Both PCA and MDS are similar techniques for data reduction but have a few important differences. While MDS tries to reduce the data in such a way as to preserve the relationships among observations or lines, PCA is meant to describe the largest sources of variance in the data. As a result, PCA can be sensitive to smaller patterns found in a single maker or a handful of markers, patterns that would not be evident from MDS.
PCA can be used to control for population stratification in association testing in two ways in JMP Genomics. The method covered in this post, known as the Eigenstrat method, is found in the PCA for Population Stratification tool. This tool performs the PCA analysis first, saving the output, and then optionally performs Eigenstrat association analysis, if one or more trait variables are specified.
- From the Genomics Starter menu, choose Genetics > GWAS Testing > PCA for Population Stratification.
- Numeric genotypes are needed for this analysis. Reference the Recode Genotypes procedure outlined in the earlier blog post, Genetic Association with JMP Genomics, Part 1: Importing and Cleaning Data.
- On the General tab, choose rice_genos_recgeno.sas7bdat, as the Input SAS Data Set.
- Assign the GW as the Trait Variable. Assign GID as the Label Variable. The traits measured are as follows:
- FL: days to flowering
- PH: plant height
- PW: panicle weight
- GW: grain yield
- Designate the other three trait variables (FL, PH, PW) as Variables to Keep in PCA Data Set. Note that this analysis can handle multiple traits at a time, but for this example, we will be building a QK mixed model for grain yield only.
- Type recgeno: in the box labeled List-Style Specification of Marker Variables.
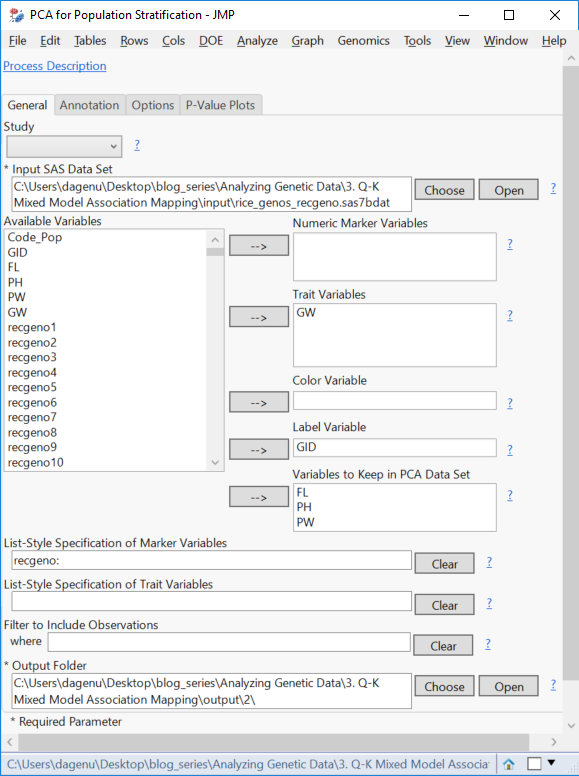
- Choose an Output Folder.
- On the Annotation tab, select rice_anno_recgeno.sas7bdat as the Annotation SAS Data Set.
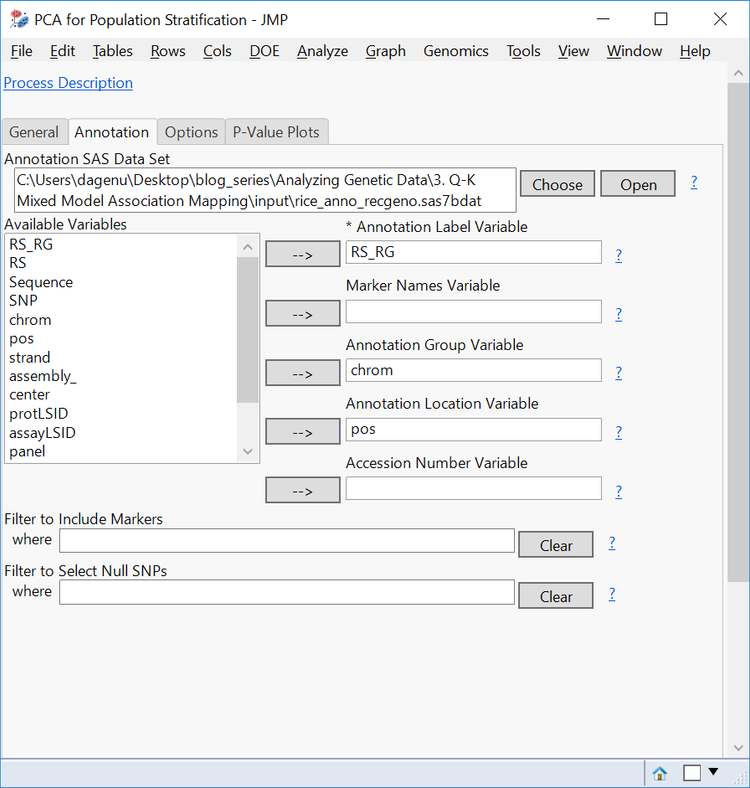
- Fill out the Annotation tab with RS_RG as the Annotation Label Variable, chrom as the Annotation Group Variable and pos as the Annotation Location Variable.
- Under the Options tab, check the box next to Create merged PCA output data set. This creates the file that will be used for QK analysis.
- Here, a PCA Data Set can be specified which is created from an earlier iteration of this process. Also, the Number of Principal Components and/or the Cumulative Proportion of Variation to Explain with PCA can be specified. Here, JMP will explain that proportion using the minimum number of components or explain as much variance as possible using the maximum number of components specified. To choose the exact number of components used, enter 5 as the Proportion of Variation to Explain.
- In this example, set the Maximum Number of PCs to 5 and the Cumulative Proportion of Variation to Explain to 5.
- Check the box to Perform EigenCorr to select PCs. This will determine which principal components to include in the regression by creating a p-value for the correlation between each PC and trait variable, and including the PCs with significant p-values based on the Multiple Testing Method and Alpha value specified. Here, select FDR and 1 respectively.
- Select Continuous from the Type of Trait dropdown menu.
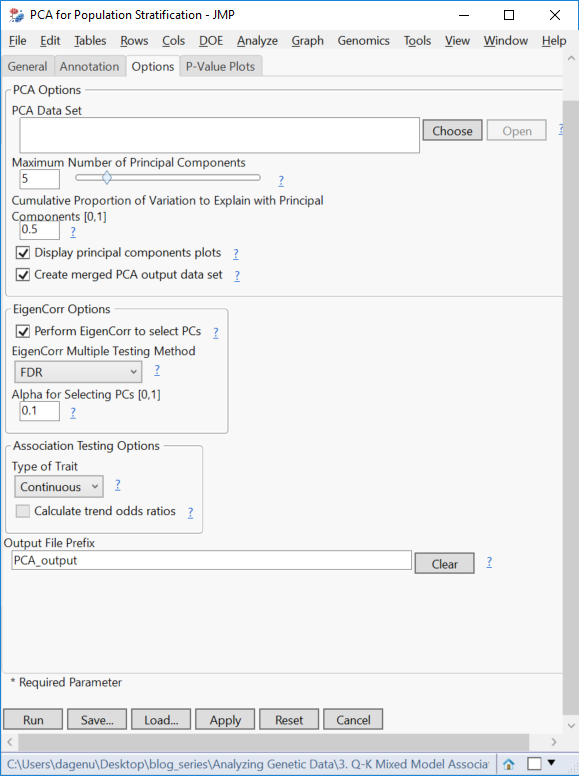
- Type “PCA_output” in the Output File Prefix.
- On the P-Value Plots tab, select -log10 for the Conversion for p-values. Note that these options affect the plots included in the SNP-Trait association output and not the actual PC selection.
- Leave the Alpha value as 0.05 and click Run to start the analysis.
Results
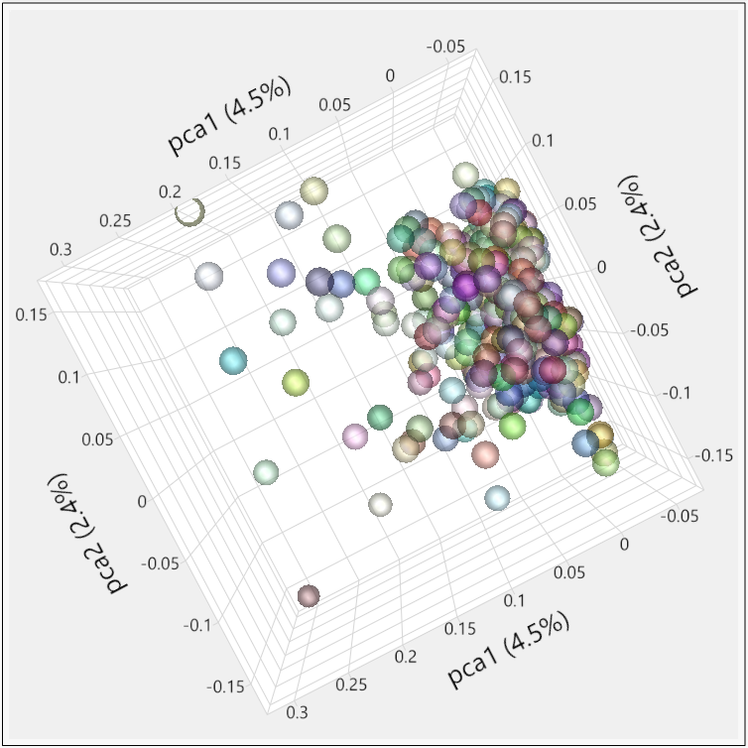
- When the results dashboard appears, both the PCA 2D & 3D Row Scores tabs show the relationships between the principal components. Individuals that cluster together in these plots would be considered to share ancestry. The 2D Plot shows the correlation of each of the five PCs with one another. In the 3D Plot, the relationship between any three PCs (selected beneath the plot) can be shown in a three-dimensional space.

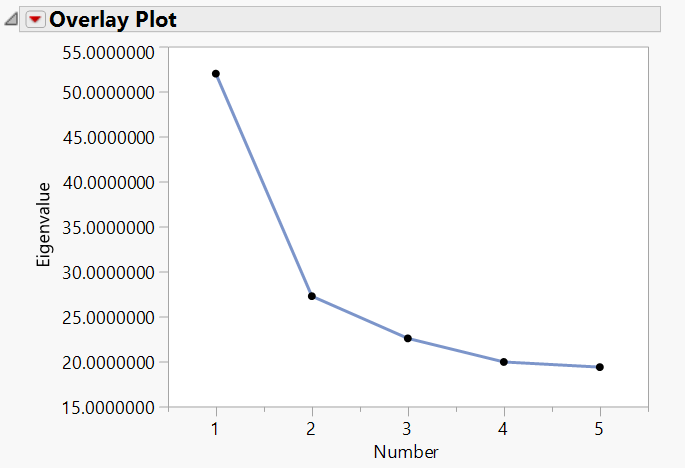
- Explore the Scree Plot. Each point in this plot represents a principal component and the amount of variation that component accounts for.
- Click on the Summary Chart tab to view results from the Eigenstrat association analysis. The bar chart shows the number of significant markers on each chromosome.
- To inspect a single chromosome, find the button for that chromosome in the Tabs section and choose View Tab.
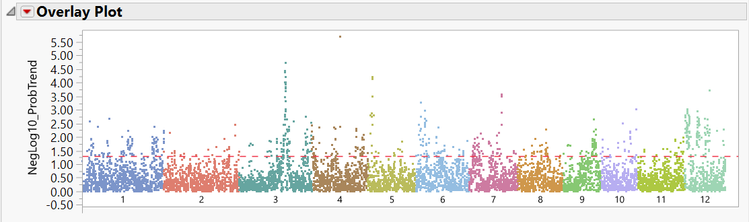
- The Manhattan Plot tab shows significant markers for grain yield colored by chromosome. Points on the plot above the red line are considered significant markers.
- Finally, the Volcano Plot tab shows a volcano plot of each marker colored by chromosome with minor allele genotype effect on the x-axis and the log transformed p-value on the y-axis. Points above the red line are considered significant.
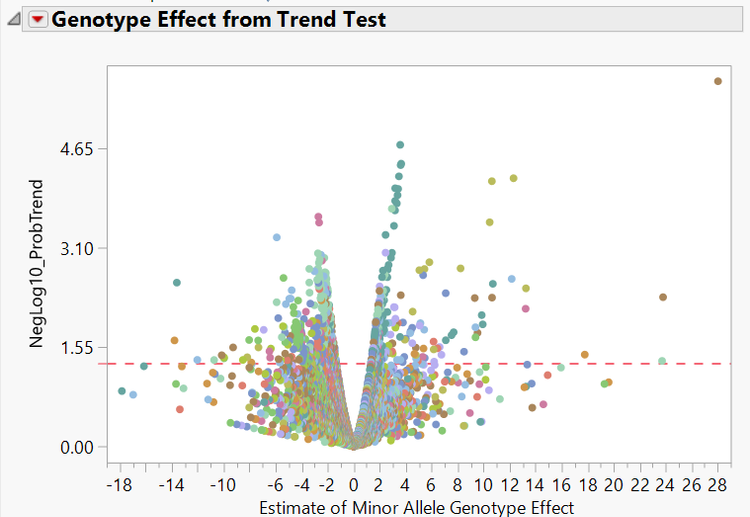
- The file pca_output_pcm.sas7bdat is now located in the Output Folder designated earlier and has the PCA values which can be used in Q-K Association Analysis.
*View the interactive results from this analysis at JMP Public.
Follow-Up Processes
This guide covered the Q-matrix portion of Q-K analysis. The Q matrix contains information about population structure, which can come from Multidimensional Scaling, Principal Components Analysis, or even manual assignment of the lines or individuals into groups curated by the user. The output data set, pca_output_pcm.sas7bdat, from this analysis can be used in Q-K association analysis. For the next step in the Q-K Association Analysis pathway, view the blog post Part 3c: Q-K Mixed Model.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.