- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
(Please note that the second version of the script offers a significant enhancement over the first version. Please download and update your copy if you got it before October 3, 2014.)
This script can be used with any numeric data column to demonstrate the beneficial effect of the Box-Cox transformation. A new column is created with the transformed variable. The new column name is the original column name with the "X" suffix. The new column includes a custom column property, Lambda, with the value of the transform parameter or power. Initially the power is 1 and the new column contains the original data values.
Note that the transform assumes no model but the log likelihood assumes the normal distribution model or equivalently the ordinary least squares regression model with only a constant intercept term.
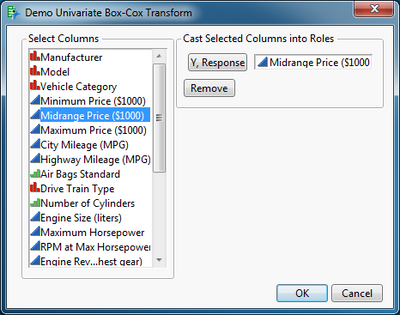
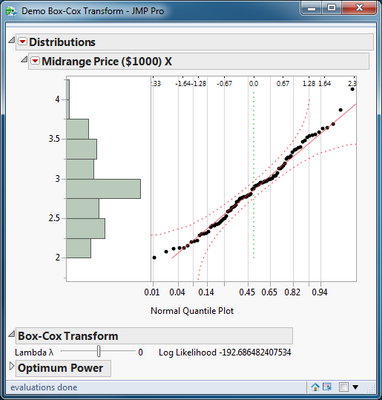
Simply open the data table with the variable to be transformed and then open and run the script. I am using the Midrange Price variable in the Cars 1993 data table as my example. Select the data column, click Y, Response, and then click OK.
The demonstration uses the Distribution platform to display the histogram and the normal quantile plot of the transformed data column.
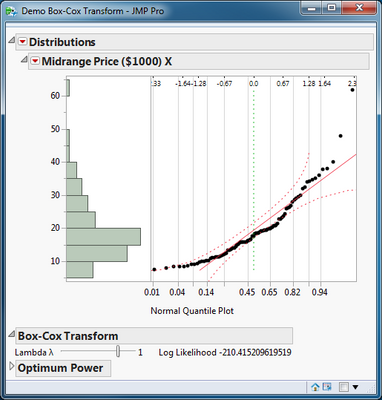
You can see in both plots that this variable exhibits a strong right skew. The log likelihood is -210.415 when the power is 1. Use the slider to change the power between -2 and 2 in 0.1 steps. The lambda value -0.2 results in the highest value of the log likelihood (-192.066).Changing lambda with the slider updates the new data column. This change in turn updates the plots because the Auto Recalc feature of Distribution is turned on.
(Note that the next part demonstrates the new feature!)
Open the Optimum Power outline.
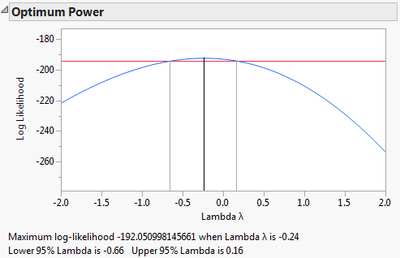
This report shows the log likelihood profile for the parameter lambda as a blue curve. The maximum log likelihood value is indicated by the black vertical line. The gray vertical lines on either side indicate the lower and upper 95% confidence interval based on a likelihood ratio test significant at alpha = 0.05. The red horizontal line intersects the curves at the interval.
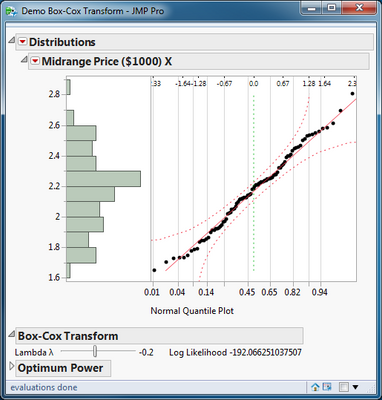
A good general practice is to round the value to the nearest whole number (0, 1, 2, et cetera) or reciprocal whole number (1/2, 1/3, et cetera) because this value usually has a physical interpretation or foundation. In this example, 0 is a good choice for lambda. This power is equivalent to the log transform and yields a slightly lower log likelihood (-192.686) and no appreciable loss of linearity in the normal quantile plot.
Note that you can obtain the same result with the built-in command in the Fit Least Squares platform if you cast the variable in the Y or response role but do not include any fixed effects (intercept only model).
Reference
6.5.2. What do we do when data are non-normal (as of October 3, 2014)
(Personal thanks to Professor Christopher Nachtsheim at the Carlson School of Management in the University of Minnesota, for help with developing this demonstration.)
(Additional thanks to my colleagues Dr. Diane Michelson and Dr. Chris Gotwalt for always pushing me for more instructional features, rigor, and better graphics.)
Wow, this is excellent, thanks so much! Is there a reason why this is not built into the JMP distribution platform?
It would be immensely useful to access a Box-Cox transformation there rather than going through Fit Model.
I agree. This would be great in the Distribution platform unless there is some reason against using Box-Cox transformations that I am unaware of.
This is a very helpful script. There are many situations when power transformation is helpful when you are not fitting a model. I don't think JMP has built in a univariate Box-Cox, yet, unless I didn't see it in JMP 15. Minitab has the univariate Box-Cox built in. Just sayin'...nudge nudge.
I am beta testing JMP 16, and the box-cox transformation is now basically in all platforms that I can see (Distribution, Fit Y by X, Fit Model). AND, even better, a little graphlet pops out to show you what your distribution would look like upon transforming at various lambda levels.
Oh that is fantastic!!!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us