Demonstrate the Distribution of P-Values

[#1]

The p-value is important in deciding to reject or not to reject the null hypothesis in a significance test. Unfortunately, p-values are also often misunderstood. This script is based on the one-sample Student's t-test of the population mean. It simulates the test statistic and its associated p-value for many samples. Any case may be simulated. That is, you can enter any population mean and standard deviation as well as the hypothesized mean.

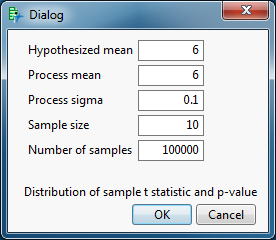
Simply open and run the script. The first time, I will simulate the case where the null hypothesis is true. In this example, an important property of the final preparation is the pH. It should be 6 (H0: mean pH = 6). The simulated population of preparation pH values has a mean of 6 and a standard deviation of 0.1 pH. I obtain the pH for 12 preparations. I will simulate 100,000 samples and obtain the t statistic and its p-value for each sample. The following dialog includes all of the correct parameters for this simulation.

Click OK.

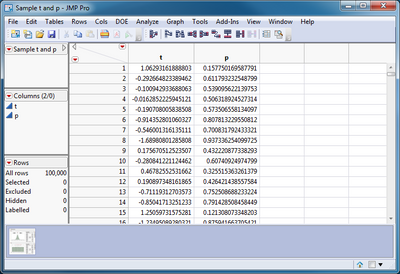
The results for each sample appears on separate rows.

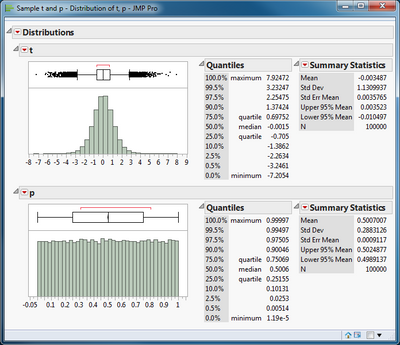
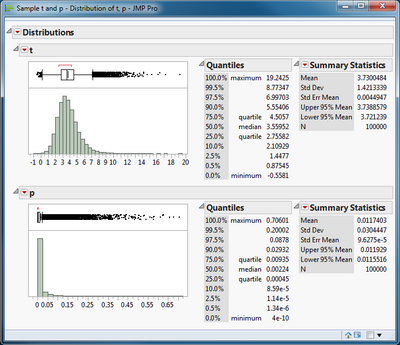
The sampling distribution of the t statistic and its p-value are displayed in a Distribution platform. There are two important features to be noted here. First, the t statistic is symmetrically distributed when the null hypothesis is true. Second, the p-value is uniformly distributed when the null hypothesis is true. That uniformity is why the rule of rejecting the null hypothesis when the p-value less than the significance level leads to a probability of a type I error equal to the chosen significance level.

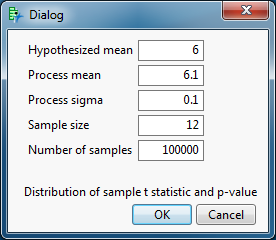
I will repeat this demonstration. This time, I will simulate the case where the alternative hypothesis is true. The only change is that simulated population of preparation pH values has a mean of 6.1. I again obtain the pH for 12 preparations. I will simulate 100,000 samples and obtain the t statistic and its p-value for each sample. The following dialog includes all of the correct parameters for the second simulation.

Click OK.

The two main features dramatically changed. The sample t statistic is no longer symmetric. This shape is known as the non-central t distribution. The p-value is no longer uniformly distributed. Many results are now below the level of significance, more than 90%. This shows the power of this test when the change in the mean is equal to one standard deviation and the sample size is 12.