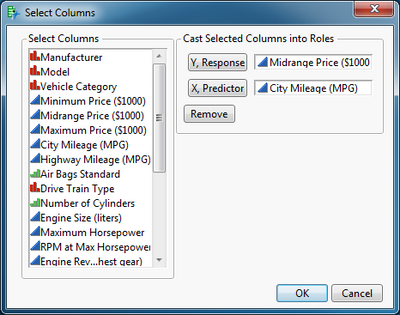
This script supports an interactive demonstration of the Box-Cox Power Transformation in the context of a simple linear regression. You can transform the dependent variable, the independent variable, or both. Simply open a data table with an example. (This description uses the Cars 1993 data table from the Sample Data folder.) Then open and run the script. Select the dependent variable and click Y, Response. Select the independent variable and click X, Predictor.
Click OK.
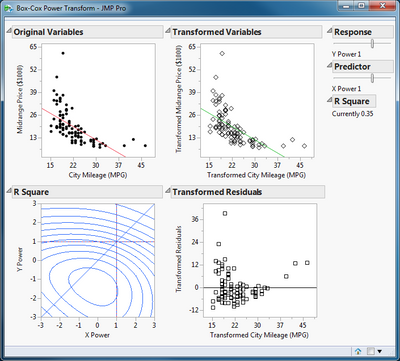
The initial result presents for plots as the main feature. These plots, starting in the upper left and proceeding in clock-wise order, are:
- A scatter plot of the original data. This example exhibits a non-linear relationship and heteroscedasticity.
- A scatter plot of the data after transformation. The power level for each variable is initially set to 1, which does not change the data.
- A scatter plot of the residual error by predictor after transformation.
- A contour plot of the R square of the regression (contours) as a function of the X and Y power level. The current power levels for the independent variable and the dependent variable are shown by the vertical and horizontal lines, respectively. The diagonal line indicates where the X and Y power are equal. The maximum R square achieves the same purpose as the minimum sum of squared errors for determining the best power. The maximum R square for this example is inside the contour in the lower center of the plot.
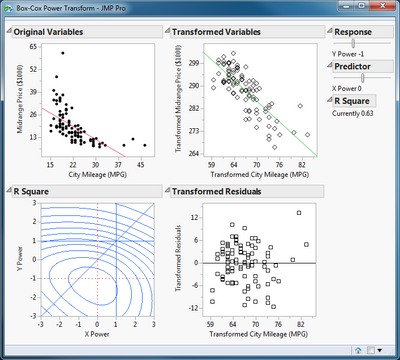
There are two sliders to the right of the plots that determine the current power value for each variable and a report of the R square for the linear regression under the current transformation. R square is initially 0.35 for this example. Drag the slider for each variable until the maximum R square value is achieved.
The R square is now 0.63, the relationship is now essentially linear, and the errors are homoscedastic.
Note that the Box-Cox Power Transformation for the dependent variable is available in the Fit Least Squares platform.
Reference
Box, G. E. P., and D. R. Cox (1964) An Analysis of Transformations, Journal of the Royal Statistical Society, Series B (Methodology), 26(2)211-252.