What is the best age to start collecting Social Security?
Created:
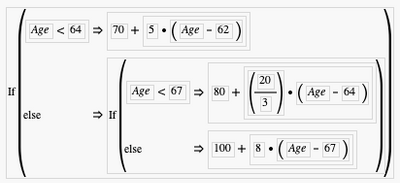
One topic that we've heard quite a bit of discussion around the Internet is when does it make most sense to start collecting Social Security. For those folks who aren't familiar with U.S. Social Security system, the basic idea is that the government provides a monthly income for those people who have contributed for a minimum number of years into the system. The monthly amount depends on how long and how much you've contributed, and it's adjusted for inflation on a regular basis. Another factor that affects how much you can collect, and what's most important for the purpose of our post, is the age at which you start collecting. Currently, you can collect as early as age 62 at a reduced rate: 70% of the amount at full retirement age (67). You can also delay collecting until age 70. Doing so lets you collect at 124% of your full retirement age benefits. The exact formula for calculating how much you collect is:
Age is rounded down to the closest month. The result is expressed in percent relative to full retirement age.
Collect less money sooner or wait to collect more?
Increases stop at age 70, which begs an interesting question, "Is it better to collect earlier, at a reduced rate but for longer, or later at an increased rate?" We'll consider two situations: 1) using the money immediately or 2) investing it. What makes this question interesting is not only does it address a retirement topic that comes up regularly, but it lets us demonstrate some nice features in data tables you might not be aware of.
First, we'll want to calculate the cumulative amount we would receive under these different scenarios. This is relatively straightforward in the immediate use cases, since it's a cumulative sum of the amount received. Values will be scaled relative to the amount collected at full retirement age to make it independent of absolute dollar amount received. Working with a column of ages beginning at 62, we can use the summation formula, making sure to correctly index the function to start at the appropriate age. For age 62:
Summation(i = 1, Row(), 0.7)The first argument to Summation is an expression that specifies the indexing variable, in this case i, along with its initialization value, 1. For this example, we're not using i, but it's commonly used for the body or upper bound of the summation and is needed for the formula to work. The formula for age 67:
If( :Age >= 67, Summation( i = 6, Row(), 1 ), 0)If we wanted to consider the case where the distribution is invested, we have a bit more work, since each year is the current contribution plus the sum of the previous contributions with interest compounded yearly (for simplicity). This can be done in a single column in at least two ways. The more obvious approach is to use the Lag function to accumulate.
If(Row() == 1, 0.7, Lag(:Age62plus0.03 * (1 + 0.03)) + 0.7)This is the formula for starting at age 62 and investing at a 3% rate. The formula is self-referential, the column listed in the Lag function is the column to which the formula is applied. In this case, self-referencing works since an initial value is set for row 1, making values available each time the Lag function needs to be evaluated (i.e., the previous row has a value associated with it).
A more compact approach, something that can account for both investing and not investing cases, is to use the Future Value function. JMP has about a dozen finance functions that are useful in situations like this. They're listed under their own group in the Formula Editor. Future Value, from its description in Help:
Returns the future value of an investment based on period, constant payments and a constant interest rate.
It has three required arguments:
Future Value(rate, nper, pmt)
where rate is the interest rate, nper the period number, and pmt the payment amount. There are two additional arguments that we will leave at their default values. For example,
-Future Value(0.03, 3, 0.7)
gives the amount accrued in the third year, invested at 3%, for an age 62 retiree (0.7 payment). Since Future Value returns a negative number, we will prefix it with a negative sign. If the above were changed to
-Future Value(0.03, :Age – retireAge + 1, 0.7)
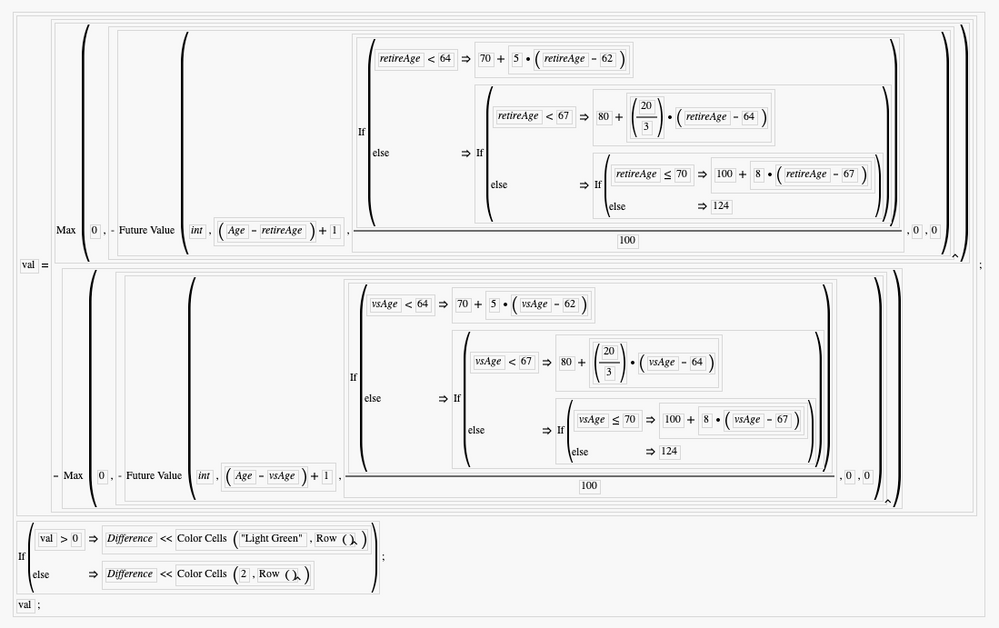
where retireAge is either the hard coded retirement age or a table variable containing the retirement age, we don't have to worry about the period number. Going one step further, if we replace pmt with the formula at the beginning of the post, we can use it for any of the retirement ages.
In this formula, int is a table variable with the interest rate. Max is used to deal with the situation where Age is less than retireAge and a negative value is returned.
Comparing retirement ages
Let's say we're interested in the difference between two retirement ages. We can create a formula that's the difference between two Future Value functions. The first will be as above. In the second, we will substitute vsAge, a table variable giving the alternative retirement age, for retireAge. Let's also say we want to interactively color positive value rows green. This can be done by treating the Formula Editor formula like a block of JSL code. To get it to work properly, you need to use multiple statements and know that the Formula Editor returns the value of the last evaluated statement. The general form will have three statements:
- variableName = Expression calculating the difference;
- Expression setting the cell color relative to variableName;
- variableName;
In the example, val is the variable name. The color is set using
If( val > 0,
:Difference << Color Cells( "Light Green", Row() ),
:Difference << Color Cells( 2, Row() )
)The first argument to Color Cells can be a standard color name or a color number. Difference is the name of the column where the formula appears, so it is self-referencing. The variable val appears at the end, so that the actual value appears in the data table.
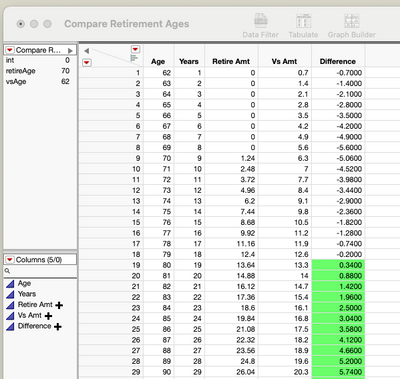
We now have a table where we can make comparisons between two different retirement ages and different investment scenarios by just changing table variables. Let's say we want to compare retiring at 70 vs. 62 without investing. We would have to wait until between ages 79 and 80 before we broke even.
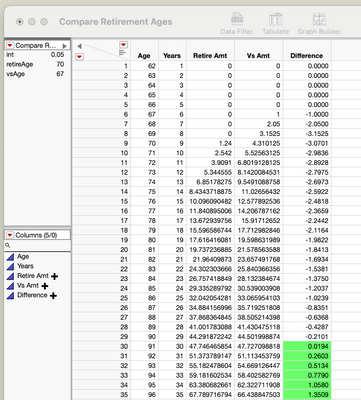
What about comparing ages 70 and 67, where the distributions are invested at 5%. Breakeven occurs between ages 90 and 91.
Final conclusion: It depends
So, what's the best age to start taking Social Security? Like the answer to many statistical questions, it depends. Delaying retirement until 70 is best if you plan on spending the distributions immediately and expect to live past 80. On the other hand, if you plan on investing the distributions and don't plan on being around past your late 80s or so, taking retirement earlier makes more sense. It all depends on how long you think you'll live. We'll leave answering that question for another time.
Comments