Repeated Measures Cov/Corr Diagnostics Add-In
Community Manager
Community Manager
Created:
| Last Modified:
This Add-In will take the unstructured repeated measures covariance and correlation matrices and report them in matrix form (rather than as a column list). The Add-In also produces a heatmap of the correlations over the time lags. These output forms make it easier to evaluate the data correlation and covariance structure to choose candidate structures to fit. This Add-In was created in collaboration with @julian, and because it builds on a repeated structure available only in JMP Pro, it will only be useful to users of JMP Pro.
The following illustration is taken as an excerpt from the new JMP for Mixed Models book, with @eclaassen and @russ_wolfinger, coming soon from SAS Press. For more information, see support.sas.com/hummel.
To use this Add-In you should first download the attached file (extension “jmpaddin”) and click on the file to open it. You will be prompted to install the Add-In. Click the Install button. You can now delete the original file. The Add-In is permanently installed in your “Add-Ins” menu in JMP.
Next open your repeated measures data file. Here we use the attached data file Respiratory Ability Stacked. This example appears as Data Set 5.2, “Respiratory Ability,” in Appendix 2 of SAS for Mixed Models, Second Edition (2006). It originally appeared in Littell, Pendergast, and Natarajan (2000) and was used in Littell, Stroup, and Freund (2002).
As described in SAS for Mixed Models: A pharmaceutical company examined effects of three drugs on respiratory ability of asthma patients. Treatments were a standard drug (A), a test drug (C), and a placebo (P). The drugs were randomly assigned to 24 patients each. The assigned treatment was administered to each patient, and a standard measure of respiratory ability called FEV1 was measured hourly for 8 hours following treatment. FEV1 was also measured immediately prior to administration of the drugs.
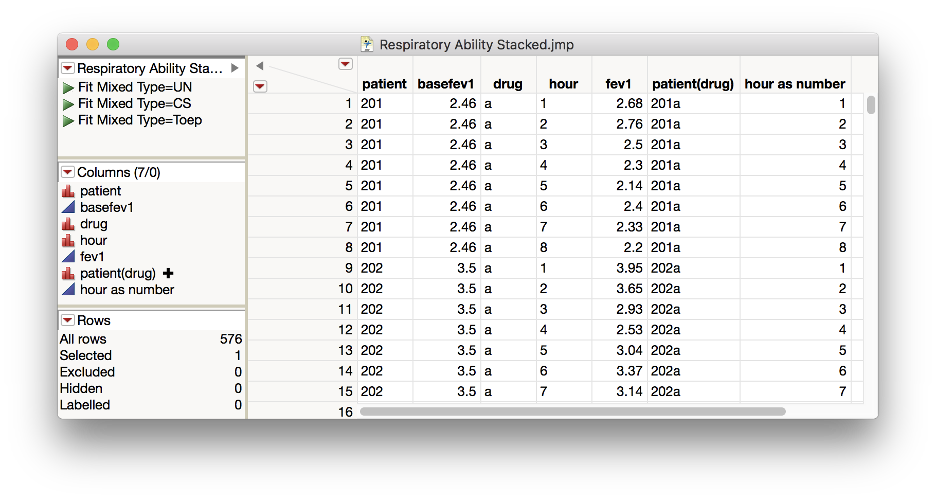
The original data table was in the long format, with different columns for each time point. (One row per patient, but the response was in eight different columns, according to the time point.) To more easily analyze the time trend, it is useful to first create a stacked version of the data, where each patient now has eight rows and the response FEV1 is now in a single column. It is also helpful to create a column “hour as number” to allow fitting covariance structures like AR(1), spatial, and Antedependent that require a continuous measurement of time. Lastly, it is helpful to create a column “patient(drug)” to uniquely identify each patient. (The patient numbers repeat for the three drug groups, but patient 201 in Drug C is NOT the same person as patient 201 in Drug P.)
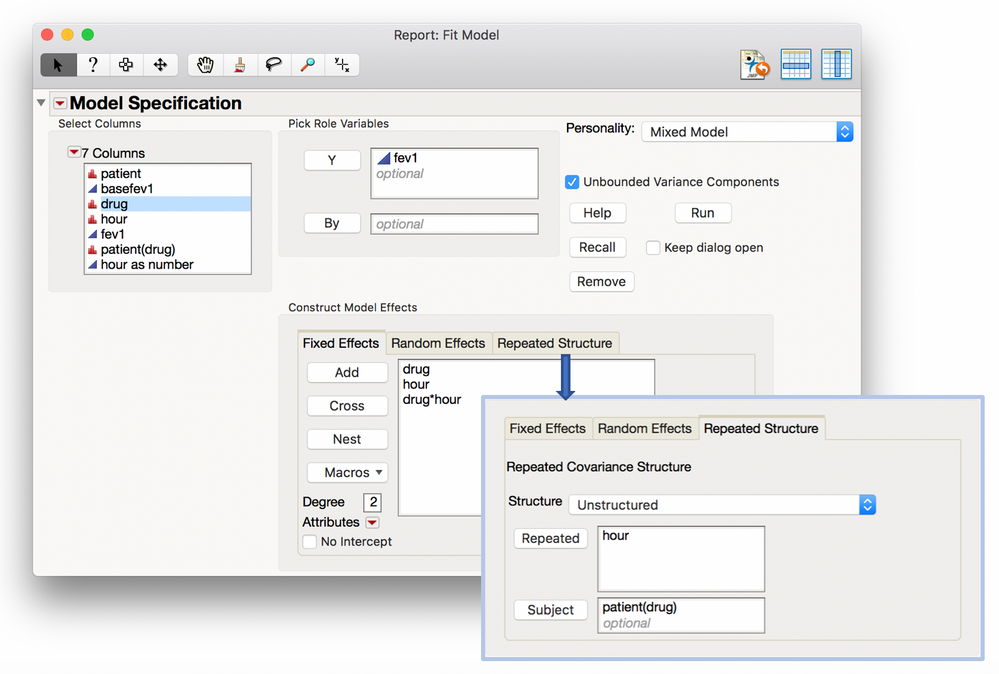
Use Analyze > Fit Model to define the model. Change the Personality to “Mixed Model” in order to see the tabs for “Construct Model Effects” that include “Random Effects” and “Repeated Structure.”
Enter “FEV1” as the Y variable. Enter “drug,” “hour,” and “drug*hour” as Fixed Effects. (You could also put “basefev1” here if you want to adjust each subject by their baseline FEV1 measurement.) You do not need to enter any Random Effects. For the Repeated Structure, select “Unstructured” and enter “hour” as the Repeated and “patient(drug)” as the Subject.
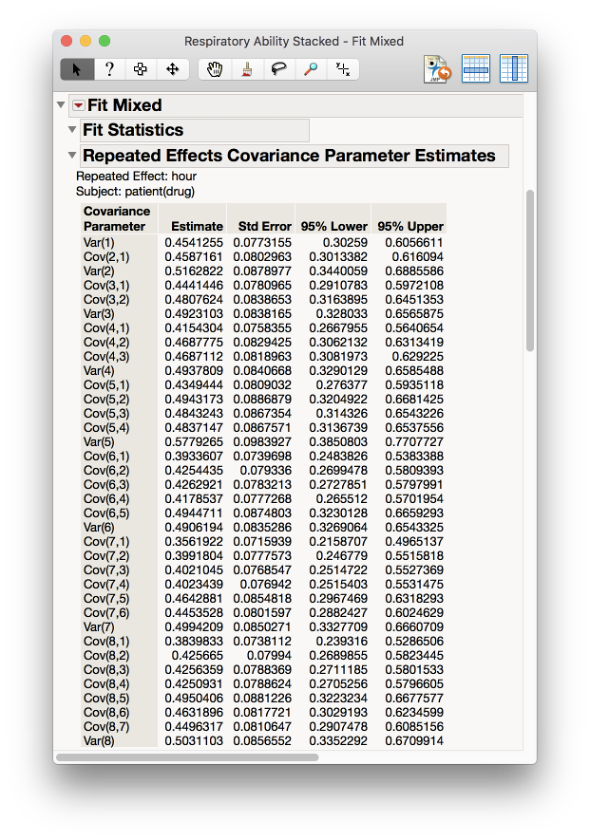
Here’s the reported variance/covariance matrix from the output:
Use of the Add-In:
Now click the “Repeated Measures Cov/Corr Diagnostics” Add-In using the button for this under your Add-Ins tab in the JMP menu bar. If you have several model reports open, you will be prompted to select the report you want to use this Add-In on.
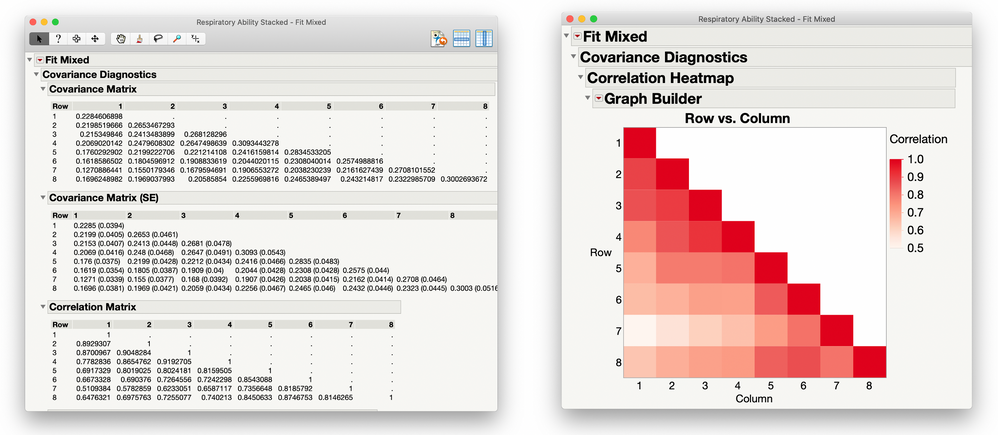
The Add-In will produce additional output at the bottom of your report. Scroll down to find the correlation and covariance matrices (including a version of the covariance matrix that reports the standard errors for those variance and covariance estimates) and the correlation heatmap.
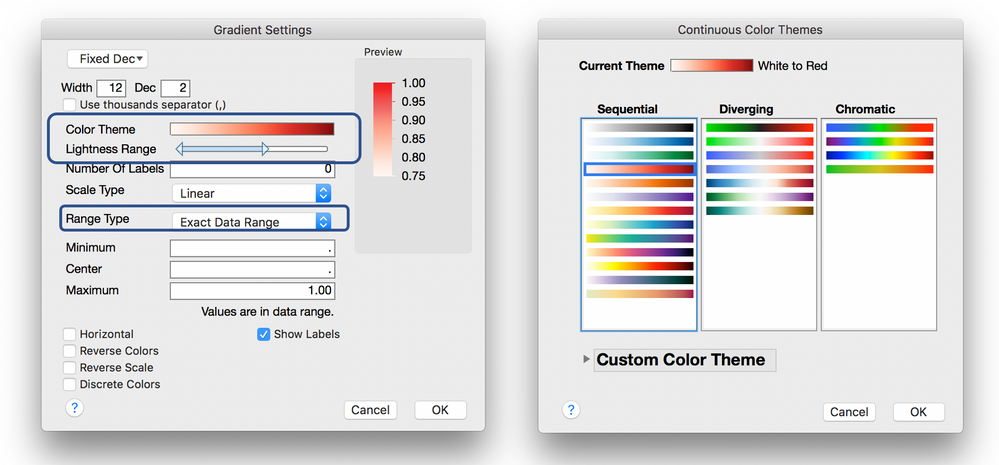
If the default color gradient on the heatmap is not very informative, right-click over the red-to-blue color scale and select “Gradient.”
Click in the “Color Theme” to select something Sequential (if you have only positive correlations, for example). Adjust the lightness range if desired. Change the “Range Type” to “Exact Data Range” to better distinguish between high and low correlations for your specific range.
Now you can use the values in the diagonal of the Unstructured Covariance Matrix to determine if the variances can be treated as equal or would be better treated as unequal. Then use the Correlation Heatmap to determine if there is a pattern as you move your gaze diagonally down and to the left.
Interpretation:
In this case, the variances for each time point (these are the values across the diagonal in the covariance matrix) range from 0.45 to 0.58. If we use the rule of thumb that standard deviations need to be at least a two-fold difference to require being treated as unequal, that would mean that these variances need to be at least four times different. By that standard, we can treat these variances as approximately equal across all eight time points. Likewise, look at the standard errors for these variances. If a 95% confidence interval for the first variance would be approximately 0.4541 +/- 2*0.0773, that would be around (0.30, 0.61). From this we can get a sense that any test of the difference between two of these variances will definitely fail to reject the null hypothesis that the variances are equal. But, keep in mind that all of these heuristics are approximate and are by nature trying to prove a null hypothesis (which we can’t do!). It would be reasonable in this case to treat the variances as equal, but it might also be worth our time to try fitting unequal variances and see how that improves or worsens the fit (judged by fit statistics).
Looking at the correlation heatmap, it seems that the correlations are pretty high for small time lags but they get systematically weaker as the time lag increases. From these observations we might consider the following options for the repeated structure:
- Compound Symmetry probably will not fit well, because it assumes no change in correlation over time lags.
- Toeplitz might fit well, although it ignores the decay relationship over the time lags.
- AR(1) (or, equivalently, Spatial Power) is a great choice, if that decay is in a power relationship.
- Antedependent is a possibility, because that is somewhat between Toeplitz and AR(1). But Antedependent will introduce a lot of new parameters, which might not be worth any small improvement in fit over a simpler model like AR(1). We can confirm this by looking at the fit statistics that penalize additional parameters (use AICc or BIC).
The resulting fit statistics of these four candidate models (all using equal variances assumption), and the unstructured, are shown here:
We are looking for a model that has low values on the fit statistics, relative to the other contenders. We can see that the Toeplitz is the best fitting model on the Bayesian Information Criterion (BIC), and it is approaching the Unstructured fit on the corrected Akaike’s Information Criterion (AICc). For these reasons, the Toeplitz is a good choice to use for the final model. We can now interpret the final model results that come from including the Toeplitz repeated measures structure.
Data References
Littell, RC, GA Milliken, WW Stroup, RD Wolfinger, and O Schabenberger. 2007. SAS for Mixed Models, 2nd ed., SAS Institute.
Littell, RC, J Pendergast, and R Natarajan. 2000. TUTORIAL IN BIOSTATISTICS: Modelling covariance structure in the analysis of repeated measures data, Statistics in Medicine 19, 1793–1819.
Littell, RC, WW Stroup, and RJ Freund. 2002. SAS for Linear Models, 4th ed., SAS Institute.
