- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
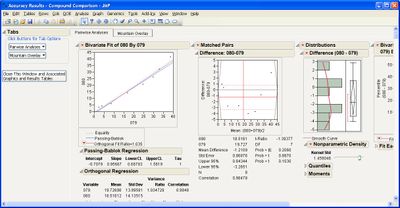
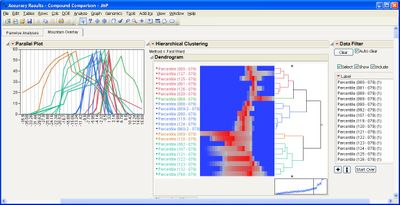
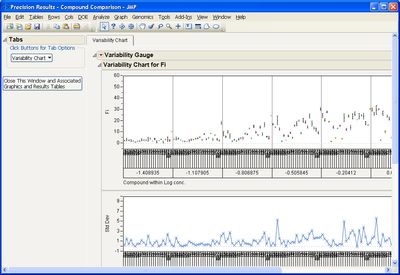
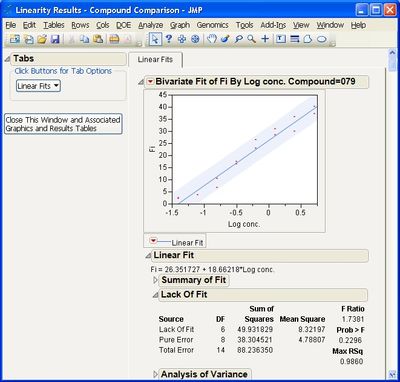
This add-in helps you compare measurement methods according to CLSI guidelines. It calls various JMP platforms behind the scenes to fit the data and create a variety of graphical and tabular results.
The add-in consists of four primary routines: Accuracy, Precision, Linearity, and Performance. The input data table to each of them must be in stacked format, that is, with one row per individual response. One column must identify the different rows of data corresponding to the different methods used (the Method Identifer column). Other required columns of data depend on the routine you use.
To install the add-in, download "Method Comparison.jmpaddin", drag it onto an open JMP window, then click "Install".
For example analyses, click Add-Ins > Method Comparison > Help after installing the add-in. The add-in also includes four example data sets: "Compound Comparison", "Peak Expiratory Flow Rate", "Simulated Example", and "Systolic Blood Pressure". Click Add-Ins > Method Comparison > Example Data to open them.
Some example screen shots are below.
Hi,
thanks for the add-in for method comparison. I have a question/remark regarding the Bland Altman plot: why is using the Std Error and not the Std Deviation (SD) to calculate the 95% limits of agreement? The use of Std Error is wrong and consequently is giving wrong limits of agreement.
Literature about Bland Altman plot and the use of Std Deviation (SD):
1. Bland JM, Altman DG. Measuring agreement in method comparison studies. Stat Methods Med Res 1999;8:135-60
2. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Int J Nurs Stud 2010;47:931-6
3.Giavarina D. Understanding Bland Altman analysis. Biochemia Medica. 2015;25(2):141-151
Hi,
What method are you using for the Confidence Intervals for the Passing Bablock intercept and slope? If it is bootstrap then please specify what type (e.g., 2.5th and 97th percentile of the distribution of the predicted Y from all the bootstrap estimates) or something else.
Thanks,
David
@sstinca Apologies for the very long delay. When we switched over to the new JMP Community website somehow I never got notified of your message. Thanks for the great catch and I just uploaded an update that includes the Bland-Altman limits using standard deviation and a shaded display on the Matched Pairs graph. Also added the Systolic Blood Pressure data example from their 1999 paper and numbers agree.
@dstokar The limits are based on the original SAS Macro code from Roche in Penzberg, Germany, which implement the method from Passing and Bablok (1983) and do not use the bootstrap. If you have good evidence the bootstrap works well here please share, and also the JSL code is open so you can see exactly what is going on and modify it as desired.
@juanpahn Suggest working through the example in the help doc, making sure you understand everything, then try it on your own data.
I am using the ‘Method Comparison’ Add-In developed by Russ Wolfinger to compare different methods to analyze ovaries using 2D and 3D ultrasound. I have two questions:
- The Deming Regression provides the confidence interval for the slope to evaluate proportional bias, but a confidence interval is not provided in the output for the intercept. I understand that we can evaluate systematic bias from the mean difference output provided underneath the Bland Altman graphs, but for completeness in our results, it would be helpful to have the CI for the intercept of the Deming Regression as well. Can this be included in the input and/or how do you recommend I ascertain the confidence interval around the intercept?
- I am uncertain what the black diamond/ lines around the periphery of the Bland Altman graphs are – it’s not clarified in the ‘Help’ section and not described by Bland Altman’s original publication. Is it possible to clarify what these lines represent?
Many thanks.
Hi Russ,
Stupid question probably, but I'll ask still...
I went through the tutorial with the example you give in the attached word document and it worked perfectly just like in your example but then when I tried with my data, I got totally confused.
I just would like to have a Passing-Bablok regression analysis done. I just need to have and equation to my curve and a correlation coefficient. My data is like the table below.
| specimen | method1 | method2 | method3 |
| S1 | 0.322613947 | 0.283500366 | 0.394930806 |
| S2 | 1.836453685 | 1.666623257 | 1.081888255 |
| S3 | 3.276624674 | 3.338295056 | 1.384727721 |
| S4 | 4.718858377 | 4.697249324 | 1.58673576 |
| S5 | 0.318644745 | 0.311580094 | 0.272826006 |
| S6 | 1.880639096 | 1.957200801 | 0.929268173 |
| S7 | 3.390383424 | 3.417362369 | 1.28341812 |
| S8 | 4.564628617 | 4.394208312 | 1.527136804 |
| S9 | 0.343720425 | 0.424129692 | 0.912531427 |
| S10 | 2.187688239 | 2.413766417 | 0.20302838 |
| S11 | 3.402107778 | 3.153607989 | 1.277589378 |
| S12 | 5.273795942 | 5.300136478 | 1.838240998 |
| S13 | 0.67104692 | 0.414658177 | 0.432221887 |
| S14 | 2.085992847 | 1.965456038 | 0.940358883 |
| S15 | 3.712645639 | 4.047605658 | 1.189165635 |
| S16 | 4.987225862 | 4.857789074 | 1.424112418 |
| S17 | 0.298670082 | -0.114521527 | 0.449896278 |
| S18 | 1.875760383 | 1.8653793 | 0.918795834 |
| S19 | 3.703566214 | 3.642433157 | 1.112434596 |
I thought maybe I needed a table like the one below and put the first column as "method identifier" and the second column in "X, concentration" or "Y, response" but then, what do I put in X or Y?
| measure | |
| method1 | 0.322614 |
| method1 | 1.836454 |
| method1 | 3.276625 |
| method1 | 4.718858 |
| method1 | 0.318645 |
| method1 | 1.880639 |
| method2 | 3.390383 |
| method2 | 4.564629 |
| method2 | 0.34372 |
| method2 | 2.187688 |
| method2 | 3.402108 |
| method2 | 5.273796 |
In the compound comparison tutorial, I don't understand what is "method identifier" and what I am supposed to put here. I guess "X, concentration" corresponds to the reference method measures and "Y, response" corresponds to the new method measures but I am not even sure of that. Any way to help? Thanks a lot
--Pierre
@Heidi_V, yikes, sorry for the long delay! There is a request in to R&D get that confidence interval on the intercept printed in JMP's Orthogonal Regression platform. Thanks for the request and please feel free to keep bugging us about it, or if you are feeling bold I don't think the calculations are too bad given what the add-in already produces. For the diamonds in the Matched Pairs platform, see page 248 of https://www.jmp.com/support/downloads/pdf/jmp9/basic_analysis_and_graphing.pdf
@Pierre, you are on the right track with stacking your data. Your first new column is the method identifier and the second one is Y. You're going to need add an X column somehow; ideally from the experiment itself or if you just don't have it I think using sequential integers (starting over within each method) should work. The examples from the add-in are good to study.
Russ,
Looking at some data and comparing to manual calculations done in excel and matlab it seems that JMP calculates the LOA as the std deviation of differences * 1.96. However the Bland-Atlman paper from 1986 calls for using a corrected standard deviation when repeated measures are used that is sc = [SD^2 + .25 (s1)^2 + .25 (s2)^2]^5
Is there a way to run the accuracy add-in that allows for repeated measures?
Hi @russ_wolfinger,
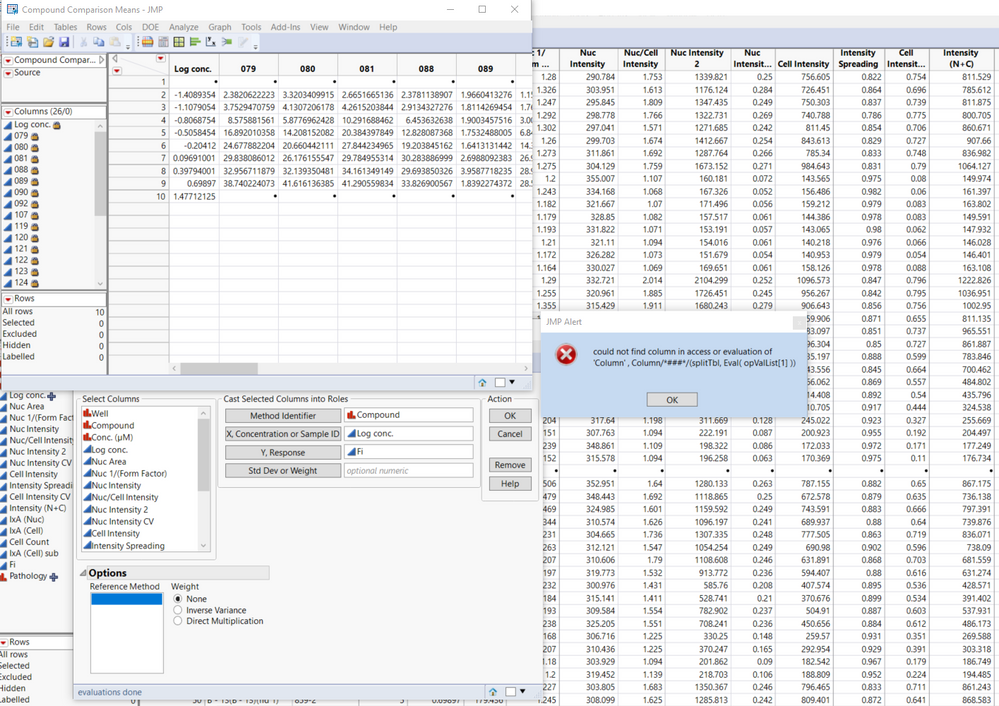
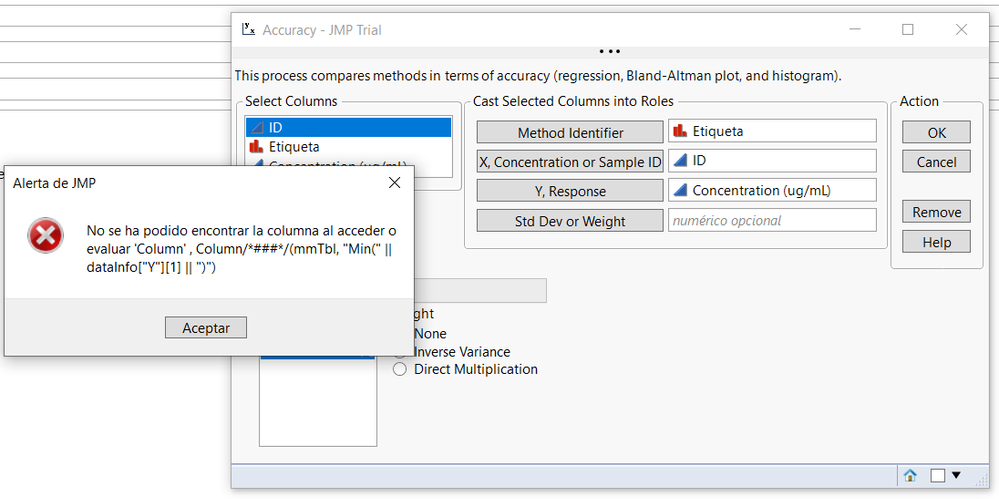
I recently downloaded the method comaprison add-in, but unfortunately, I can't get it to work. I installed the add-in and followed the first example using the provided data table. After hitting OK, I get the following error message:
could not find column in access or evaluation of 'Column' , Column/*###*/(splitTbl, Eval( opValList[1] ))
Any help would be much appriciated.
Thanks,
Hans
Hi @Hanz, In the dialog, that lower left box below "Reference Method" should be populated with values, so it appears something has gone wrong from the start. From a freshly launched JMP session, please reopen the Compound Comparison data, then click Add-Ins > Method Comparison > Accuracy. Select Compound and click "Method Identifier". The lower left box should populate with values "079", "080", "081", ... Please check your JMP log (Ctrl-Shift-L) and send any messages. (From the error message you are currently getting after going further, opValList[1] should evaluate to "079" and find that column in the Means table.) What version of JMP are you running? Are you using any regional settings or language preferences? What version of Windows?
Hi Russ!
I am using the Method Comparison Add-in to fit a Passing-Bablok regression. The add-in works great because it also adds CI's for the regression estimates which is requested by many regulatory bodies. It also computes an additional orthogonal fit for comparison.
Now I am trying to calculate the predicted value at a given X point, with Confidence Intervals using the PB fit. Is there a way to do this? because the PB fit does not have a red triangle with options.
Thanks!
Dave
Hi @russ_wolfinger ,
Thanks for your fast response. Relaunching JMP worked!
I noticed now that the Action button "Remove" acts as a kind of refresh. In other words, after adding the method identifier, I have to hit "Remove" to update and populate the dialog box in the lower left corner. Afterwards, I can proceed with the analysis as described in the help document.
For your info, I'm running JMP 12.1.0 (64-bit) on a Windows 10 Enterprise 64-bit system with no regional settings (that I know of) and English as the default language.
Now, I moved on to my own data, but apparently I still don't quite understand how to correctly format the input table after studying the example data. Since Pierre previously asked a similar question, I think it would be worthwhile bringing it up again.
In my experiment, I am repeatedly (different donors) measuring two molecules/analytes with methods 1 and 2. Method 1 is the established reference and I want to compare it to the results from method 2. Currently, my table is formatted like this:
Col1: Donor
Col2: Analyte
Col3: results method1
Col4: results method2
Example:
| Donor | Analyte | Method1 | Method2 |
| 1 | 1 | 142 | 143 |
| 2 | 1 | 143 | 141 |
| 3 | 1 | 142 | 142 |
| .... n = 40 | 1 | 118 | 120 |
| 1 | 2 | 3.04 | 3.05 |
| 2 | 2 | 4.49 | 4.39 |
| ... n =40 | 2 | 6.05 | 5.8 |
Now I would like to compare method 1 & method 2 for each analyte, and get a separate regression and Bland-Altman plot for each analyte.
Do you have any hints on how to format the table correctly?
@vtkm, apologies for the long delay in replying. I've just had the chance to look back at the standard deviation adjustment formula you reference from Bland and Altman (1986). When moving to repeated measures, there are choices regarding the assumed form of covariance structure among the observations. Bland and Altman appear to make a certain assumption along these lines that involves a form of heterogeneity between the two methods, as evidenced by their use of s_1 and s_2 (btw, I could not exactly reproduce the 21.6 and 28.2 values they indicate for s_1 and s_2 in their PEFR example, the data for which is included with this add-in under Example Data). Their adjustment formula also only applies to two repeated measures and perfectly balanced data. A better and more general approach would be a mixed model analysis that considers a few reasonable covariance structures and computes appropriate standard deviations based on a well-chosen one. Refer to recently released SAS for Mixed Models by Stroup et al. for full theory and applications + JMP Pro has good mixed model capabilities that could be utilized here. This add-in analyzes the means across repeated measures directly, which I think is still reasonable in many cases, and a natural default.
@david_arteta, no direct way to get at these. One easy thing to try would be to create your own formula column using the Passing-Bablok intercept and slope estimates. More ambitious would be to parse these values out from the appropriate table box using JSL. The ultimate would be adding the red triangle as you indicate. I'm not planning to tackle this any time soon so if anyone is willing to give it a go I'd be happy to incorporate updates into the add-in. Alternatively, it may be a good time to be voting for the formal addition of Passing-Bablok to the JMP Bivariate platform.
@Hanz, you need to transpose your data to have columns Donor, Method, Analyte1, Analyte2, then analyze Analyte1 and Analyte2 separately as the Y variable.
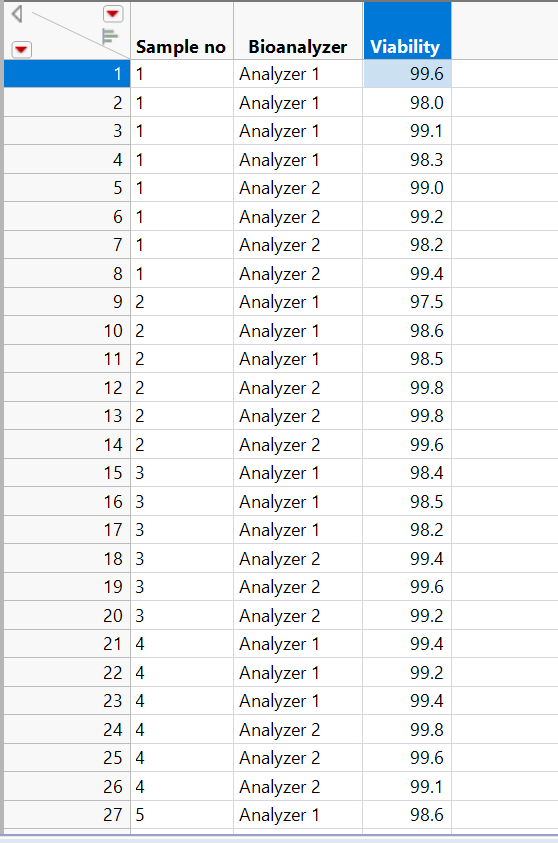
Hi, @russ_wolfinger ,
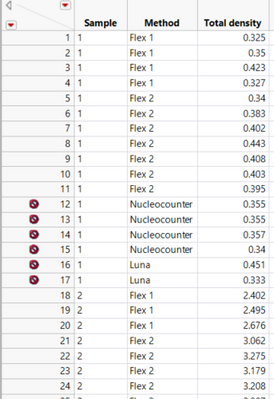
I am trying to perform Bland-Altman plot and Deming regression.
I have data in format like below:
I am receiving an error like:
Any idea what is going on...?
Regards,
Agnieszka
Hi @A_Tomczyk , Would you be willing to send me the JMP table and I can investigate further? Please attach it here or email me at russ.wolfinger@jmp.com. Kindly, Russ
I have a trial version of JMP 15 and I have problems with Accuracy test (I downloaded the add-ins from this page). I have a JMP alert when I run the test:
The alert says: The column has not been found when accessioning or evaluating “Column”.
Could help me?
Thanks
Hello @ainhoa , This likely has something to do with Spanish language settings. Would you be able to send your JMP data table so we can investigate further? Please email it to russ.wolfinger@jmp.com. In the mean time, if you would also please check if you can run the first example in the help document using the Compound Comparison data provided. In addition, if you happen to have access to a machine with English settings please try it there. Sorry for the bother--we'll work towards a resolution for you.
Thanks a lot @russ_wolfinger . I'll send you the table by e-mail and I'll try to do what you have proposed.
Hello everyone,
I have found trigger for why the "Reference method" is not correctly populated when selecting Method Identifier:
If you drag-and-drop Compound into the field, Reference method is not populated, but if you select Compound and click on the Method Identifier button, Reference method is correctly populated.
Best regards,
Helge
Thank you Helge, yes, the button does this extra work and it should be used instead of drag-and-drop. Russ
Hi, @russ_wolfinger ,
I am trying to perform Bland-Altman plot and Deming regression.
I have data in format like below:
I receiving an error:
Could you please help me with this issue?
Regards,
Joanna
Sorry, here is the data format:
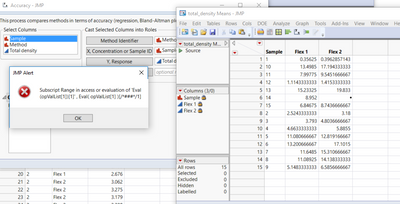
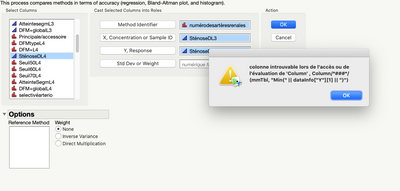
Hi, @russ_wolfinger ,
It seems that i have the same problem than ainhoa.
Indeed, when i perform method comparison and accuracy test with my datas i have the following error message:
Can you help me?
Thank you
@jzawadzka Apologies for the long delay. Would you be willing to send the full JMP table to russ.wolfinger@jmp.com ? I can try to reproduce the error and implement a fix. Based on what you sent I'm not sure what is happening.
@Etienne-88 this almost surely has to do with language settings. Note the error message is searching for column "Min" where on your machine this would be in French. The add-in has only been developed for English and I have not yet had the chance to implement a fix that would be language agnostic. One idea for a fix is to reference the column by number rather than name. In the mean time, you have access to the JSL by clicking View > Add-Ins and could potentially modify the code to work.
Hi @russ_wolfinger,
first and foremost, thank you for putting together this great add-in, I am finding it extremely useful for a project I am working on.
I was hoping to pick your brain on a related matter.
Based on my readings/customer's advice/very informative presentation by Anja Wörner, Roche Diagnostics GmbH from a recent JMP Summit, these method comparison regression approaches rely -as a condition for use- on successful Test of Linearity by Cusum Test. I believe implementation of the JMP CUSUM was in fact part of Anja's presentation but I don't seem to be able to retrieve that information.
Would you be able to help guiding me on how to implement this in JMP?
Uber grateful for your help
Very best
Camilla
Hi @CamillaLiscio Thanks for your inquiry. Unfortunately the CUSUM linearity test is not available in the add-in, but it is possible to compute it using JSL after running Passing-Bablok. Even better, I am happy to report that @jianfeng_ding is working on adding Passing-Bablok regression and the CUSUM test officially to JMP 17. It will likely first be available in one of the forthcoming Early Adopter versions (7 or 8), which you can request at jmp.com/earlyadopter
Thank you very much @russ_wolfinger for letting me know. Infact I am already using the Early adopter version so will have a look
Very best
Camilla
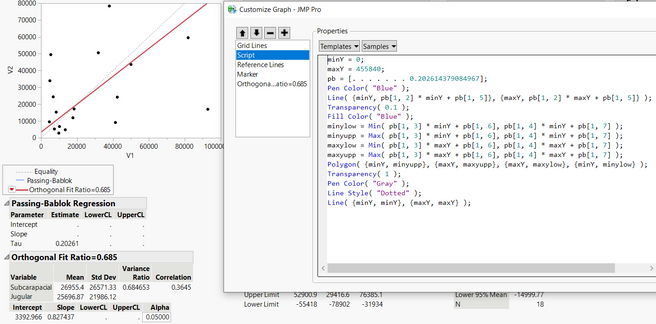
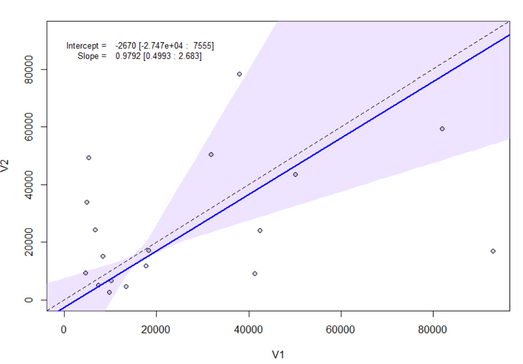
I have been using passing-bablok with the JMP Pro 16 add-in. However, the program only performs the regression for half of my data, but not for the other half despite no errors popping up. See missing slope, intercept, and confidence limits below. It performs the matched pairs/bland-altman fine for all of my data. To check if my data was at fault for passing-bablok, I used the MethComp R package and found that it was able to perform the regression while JMP was unable to do so. Would appreciate any suggestions for resolving this in JMP since the R package seems to calculate the confidence intervals differently (I learned this by testing the data that did work in JMP) Thank you!
Hi @Querida There's a chance here of numerical instability due to the large size of the values. Please try dividing V1 and V2 by 10000 to see if that helps and check the JMP log (Ctrl+Shift+L) for any messages. If no good, please send the data to russ.wolfinger@jmp.com and I can investigate further.
Hi @russ_wolfinger ,
First of all, thank you for creating this add-in! I just discovered it but I can tell it will be extremely useful in my daily work.
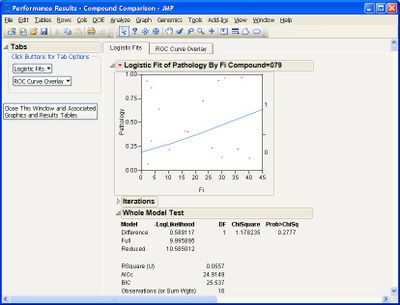
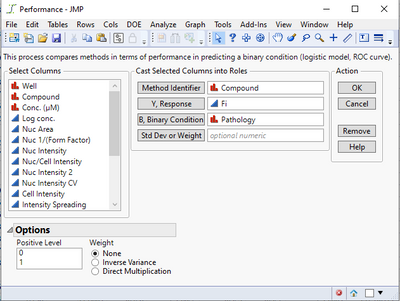
I've encountered a problem with the "Performance" analysis option. I followed the instructions on the example document, but I did not get any results. Here is what I input:
And here is the output:
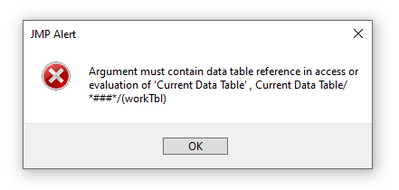
If I make any selection under the Logistic Fits option, I get the following error message:
Can you advise how to address this? I have tried restarting JMP. I have JMP version 16.0.0, if that is at all relevant.
Thanks!
@jzawadzka @Querida I just uploaded an update to the add-in that better handles missing data in the Passing-Bablok routine and will likely fix the problems you mention.
@TCGM Not sure yet what might be causing this--are there any messages in the JMP log (press Ctrl-Shift-L to see it)? In the initial Performance dialog, the value 1 should be selected by default as the Positive Level in the lower left box--does it help if you manually select it before running? Do you by chance have any non-English language settings?
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us